A 45 45 90 triangle has unique properties. Here's a good strategy for solving multiple-step geometry problems that involve it.
A right triangle has one angle which is 90°, so the sum of the other two angles must be 180°-90°=90°.
There are a couple of combinations of these other two angles that lead to special right triangles, with interesting properties.
For example, if one of the remaining, non-right angles is 45°, the other one must also be 45° (90°-45°=45°) and we have a triangle that is both a right triangle and an isosceles triangle (since both its base angles are equal to 45°).
This triangle is often called a 45 45 90 triangle. Such triangles are formed by the diagonals of a square. Let's look at a problem in which this is useful.
Problem
Find the length of segment AC in the following polygon
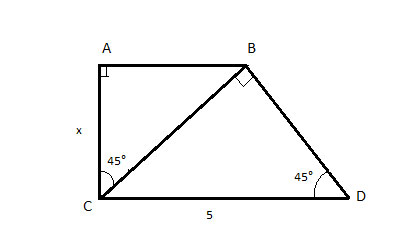
Strategy
Let's look at the hints given in the problem. The polygon is made up of two right triangles (indicated by a square angle marker), and we are asked to find the length of a line segment which is a leg in one of them. This is a hint to use the Pythagorean theorem.
But we can't apply it directly since we don't know anything about the sides of triangle ΔABC. We do know the length of the hypotenuse of ΔBCD. So we can start by applying the Pythagorean Theorem to it and finding the length of its legs.
Then, in the second step, we can use the lengths we found for the first triangle and apply the Pythagorean Theorem again, to the right triangle ΔABC.
This is called a multi-step problem, where we solve one problem first (finding the edges of ΔBCD) as an intermediate step, and then apply the results to another triangle.
But to apply the Pythagorean Theorem to ΔBCD we need more than just the length of the hypotenuse. We need one more side. This is where the next hint comes in. The angle ∠BDC is 45°, which means that ΔBCD is isosceles. So both legs are equal, CB=BD. We can set their length to 'y', and solve this problem algebraically.
And the same is true for ΔABC: ∠BCA is 45°, which means that ΔABC is isosceles in addition to being a right triangle. So knowing just the hypotenuse will be enough to find the legs.
So we've used the unique properties of a 45 45 90 triangle for solving a multiple-step geometry problem that involves it.
Solution
(1) ΔCBD is a right triangle //given
(2) m∠BDC = 45° //given
(3) m∠BCD = 45° //sum of angles in a triangle is180°, and the other two angles are 90° and 45°
(4) ΔCBD is isosceles // (2), (3)
(5) BC=BD=y //defintion of isosceles triangle
(6) 5² = y² + y² // Pythagorean theorem.
(7) 25 = 2y²
(8) √(25/2) = y
(9) y = 5/√2
(10) ΔCAB is a right triangle //given
(11) m∠ACB = 45° //given
(12) m∠ABC = 45° //sum of angles in a triangle is180°, and the other two angles are 90° and 45°
(13) ΔCAB is isosceles // (11), (12)
(14) AC=AB=x //defintion of isosceles triangle
(15) CB² = x² + x² // Pythagorean theorem.
(16) 25/2 = 2x² //Substitution, (5), (9)
(17) 25/4 = x²
(18) x=√(25/4)= 5/2 = 2.5
