Today we'll discuss one of the simple applications of the Pythagorean Theorem: finding the lengths of the edges in a right triangle.
The most common application of the Pythagorean theorem is to use the known lengths of two of the sides of a right triangle to find the length of the third side, using algebra and the formula a² + b² = c².
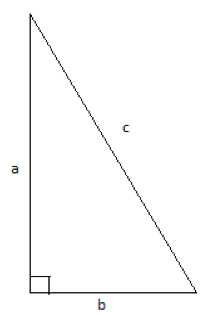
Problem 1
In a right triangle, one of the legs (a) measures 4 units, the other leg (b) measures 3 units. Find the length of the hypotenuse, c.
Strategy
This is a straightforward application of the Pythagorean theorem. We know the lengths of sides a and b, so we simply plug these lengths into the formula a² + b² = c².
Solution
a= 4, b=3 //given
4² + 3² = c² // simple substitution
16 + 9 = c²
25 = c²
√25 = c
c = 5 //c is a side length, it must be positive, so we use only the positive root.
We can also use this formula to find the length of either one of the legs, if we know the length of the hypotenuse and the length of the other leg. For example:
Problem 2
In a right triangle, one of the legs (a) measures 12 units, the hypotenuse, c, measures 13 units. Find the length of the other leg (b)
Strategy
Just as we did above, since we know the lengths of side a and the hypotenuse c, we simply plug these lengths into the formula a² + b² = c².
Solution
a=12, c=13 //given
12² + b² = 13² // substitution
144 + b² = 169
b² = 169-144=25 //rearranging
b= √25
b = 5 //b is a side length, it must be positive, so we use only the positive root.
