Finding the Area of an Isosceles Triangle

In this lesson, we will show an easy strategy for solving the following problem: how to find the area of an isosceles triangle.

Let's put into practice a number of the properties we've proven so far, in the following geometry problem:

Problem

In an isosceles triangle, ΔABC, with leg length 10, the height to the base is equal to two-thirds of the base. Find the area of the triangle.

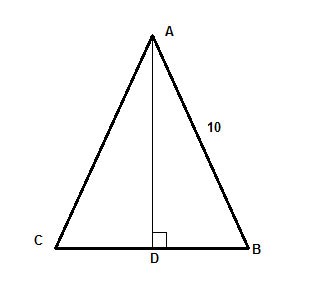
Strategy

To solve this problem, We'll work backward from what we need to do.

We need to find the area of the triangle which we know is given by the formula (base times height)/2.

An issue we have is that we don't know either the base length or the height. But, we are given the relationship between them, which is the hint on what we need to do. Let's call the length of the base, BC, x.

Then we know the height, AD, is 2x/3, as given in the problem.

So the answer we are looking for is (base times height)/2, or x times 2x/3, divided by two.

But how do we find x? There are two additional things we were given in the problem which we haven't used yet- the length of the leg (10), and the fact that this is an isosceles triangle. We probably need to use these two things to solve the problem.

Let's review the properties of isosceles triangles. One thing that should immediately jump to mind is that as we have shown, in an isosceles triangle, the height to the base bisects the base, so CD=DB=x/2.

Finally, AD is the height, which means that the angle ∠ADC is a right angle, and we have a right triangle, ΔADC, whose hypotenuse we know (10) and can use to find the legs using the Pythagorean theorem, c² =a²+b^2,

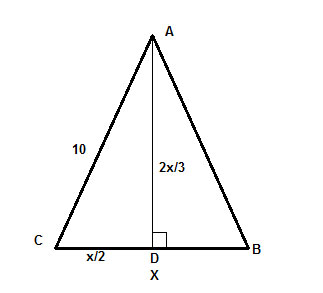
where c= 10 ,a = x/2 and b=2x/3 . And we are done,  the rest is just algebraically solving for x.

Proof

(1) ΔADC is right triangle  //given,  as AD is the height to the base

(2) AC² =CD² +  AD²          //Pythagorean theorem

(3) AC= 10                        //given

(4) CB = x

(5) CD = x/2                       //Height to base in isosceles triangle bisects the base

(6) AD = 2x/3                     //given

(7) 10² = (x/2)² + (2x/3)²    //Substitute into (2)

(8) 100 = x²/4+4x²/9           //simplify

(9) 100*36 = 9x² +16x²       //multiply both sides by 36

(10) 100*36 = 25x²             //collect similar terms

(11) 4*36 = x²                     //divide by 25

(12) √144 = x                      //take square root of both sides

(13) 12 = x = CB

(14) AD = 2x/3 = 2*12/3 = 8

(15) Area  = 12 * 8 / 2 = 48

And this is how you can easily find the area of an isosceles triangle!