The diagonals of squares are equal to each other, they bisect each other, and they are perpendicular to each other. Here, we'll show this last property.
Just like rectangles are a special type of parallelogram, squares are a special type of rectangles, in which all the sides are equal. Or you can think of it as a special type of rhombus (diamond) in which all the angles are right angles.
Because all squares are also both rectangles and diamonds, they combine all the properties of both diamonds and rectangles.
In a rectangle, the diagonals are equal and bisect each other. And in a diamond, the diagonals are perpendicular to each other. So in a square all of these are true. The diagonals are equal to each other, they bisect each other, and they are perpendicular to each other. We will now show this last property.
Problem
In a square ABCD, prove that the diagonals are perpendicular. Show that AC⊥BD
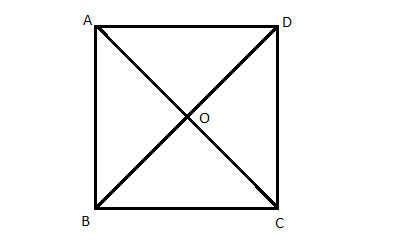
Strategy
We could do this from scratch. We can prove that any two of the adjacent triangles formed by the intersecting diagonals are congruent. Thus, the angles formed by the intersection of the diagonals are congruent and form a linear pair.
But instead, let's save some work, and use what we have already proven for isosceles triangles - that the median to the base is perpendicular to the base, and that in a parallelogram, the diagonals bisect each other.
Combining these two, we see that since the diagonals bisect each other, they form medians in the isosceles triangle ΔABC, and are thus perpendicular.
Proof
(1) ABCD is a square //Given
(2) AB=BC //Definition of a square
(3) ΔABC is isosceles //(2), Definition of an isosceles triangle
(4) AO=OC //A square is a parallelogram, diagonals of a parallelogram bisect each other.
(5) AC⊥BD //In an isosceles triangle the median to the base is perpendicular to the base.
