Area of Similar Triangles

The area of a triangle is given by the formula (base x height)/2. If we have similar triangles, their sides are proportional with a ratio given by a number called the scale factor.

The same scale factor also applies to other lines in the similar triangles - like their height, or to a combination of those lines like the perimeter.

The area of similar triangles is also proportional, but here the scale factor will be squared - because we are multiplying two line segments (base and height) which are both proportional, and have the same scale factor.

Problem

In the following drawing, AD is parallel to CB, and CD is perpendicular to AB. Find the area of triangle ΔAED.

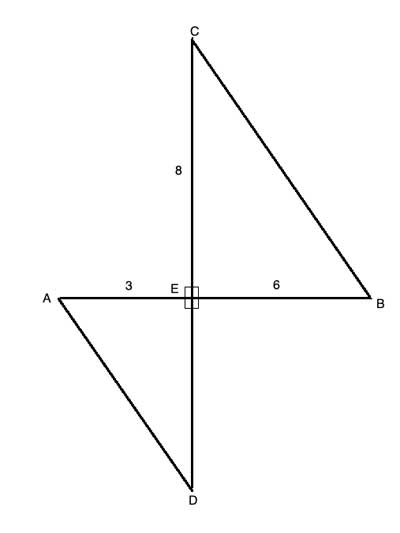
Strategy

The area of ΔBEC is (base x height)/2, and both the base and the height are given (CE is the height because CE is perpendicular to EB).

The hint in the problem is that AB||CD, so we can use our knowledge of angles created between parallel lines and an intersecting transversal line to show that the two triangles are similar.

∠DAE ≅ ∠CBE, as alternating interior angles between two parallel lines, and as m∠AED=m∠BEC=90 °, ΔAED∼ ΔBEC. The scale factor is BE/AE=6/3=2

We can now either use the scale factor to find the length of ED (ED/AE=CE/EB or ED=8/6 x 3= 4) and then use the formula for an area of a triangle (base x height)/2 to find the area, or find the area of triangle ΔBEC, whose base and height are given, and then use the scale factor squared to find the area of ΔAED.

Solution

(1) CD⊥AB //Given
(2) m∠AED=m∠BEC=90° //(1), definition of perpendicular lines
(3) AB||CD //Given
(4) ∠DAE ≅ ∠CBE //Alternating interior angles between two parallel lines
(5) ΔAED∼ ΔBEC //Angle-Angle
(6) ED/AE=CE/EB //corresponding sides in similar triangles
(7) ED=8/6 x 3= 4 //CE=8, EB=6, AE=3, given
(8) Area_AED=ED x AE /2 //Formula for area of a triangle
(9) Area_AED=4 x 3 /2 = 6

or

(8) Area_BEC = CE x EB / 2 //Formula for area of a triangle
(9) Area_BEC= 8x 6 /2 = 24
(10) Area_AED = Area_BEC/4 //Area of similar triangle is proportional to scale factor squared
(11) Area_AED=24/4=6