Area of a Heart Shape | Geometry Help

When studying the topic of "area", a geometry question that comes up frequently is how to find the area of a non-standard shape. In this post, we'll solve a common example - a heart.

A "heart" is not a well-defined description. We have wide hearts like this:

And narrow hearts like this:

So when solving this problem, unless we have some specific measurements or instructions that say otherwise, we will need to make some simplifying assumptions.

Problem

In the shape below, D is the length between its bottom tip and the bottom of the indent between the rounded areas. Find the shape's area.

An illustration of square with semicircles in blue.

Strategy

In this case, we will assume that the "heart" is made up of a square with two semicircles attached to its sides. then, we will use the strategy of breaking down a complex shape into the simple shapes that make up its parts.

With that assumption, we have a square, whose area is given by the formula A_square=a², and two semicircles. The distance D is simply the square's diagonal.

The area of each semicircle is given by the formula A_semicircle=π*r²/2. And in our case, the diameter is simply the side of the square, a, so r=a/2

To find the length of the side, a, from the diagonal, D, we divide by √2, as we have shown here - How to find the side of a square from its diagonal.

So, the area of the square is a²= (D/√2)²=D²/2. The area of each semicircle is π*r²/2= π*(D/2√2)²/2, and we have two of them, so together, the area of the two semicircles is π*(D/2√2)²=π*D²/8

And the total area is A_square+2A_semicircle = D²/2+π*D²/8=(1+π/4)D²/2

A real-life application

Students of geometry sometimes complain that they will never need to use this material in real life. I have tried to provide some hypothetical uses in problems like finding the amount of side wall needed to fence an ice rink by calculating its perimeter, but for this problem, a real use case has presented itself.

I was contacted by Chris Donahue who wanted to create a special memorial for the victims of the 9/11 terrorist attack. Chris lives on a lake in Michigan, and wanted to place 2,977 small US flags on his front lawn, one for each victim, in the shape of a heart. The flags would be spaced 1 foot apart. He wanted a perfectly sized and shaped heart, and the problem was - how big should the heart be?

Here's how I approached this problem.

The flagsticks in the ground form an equally spaced grid, with grid points 1 foot apart. Let's look at the square part first. For a square that is 1 foot by 1 foot (an area of 1 square foot) we need 4 flags. For a square that is 2 ft by 2 ft (an area of 4 square feet) we need 9 flags and so on:

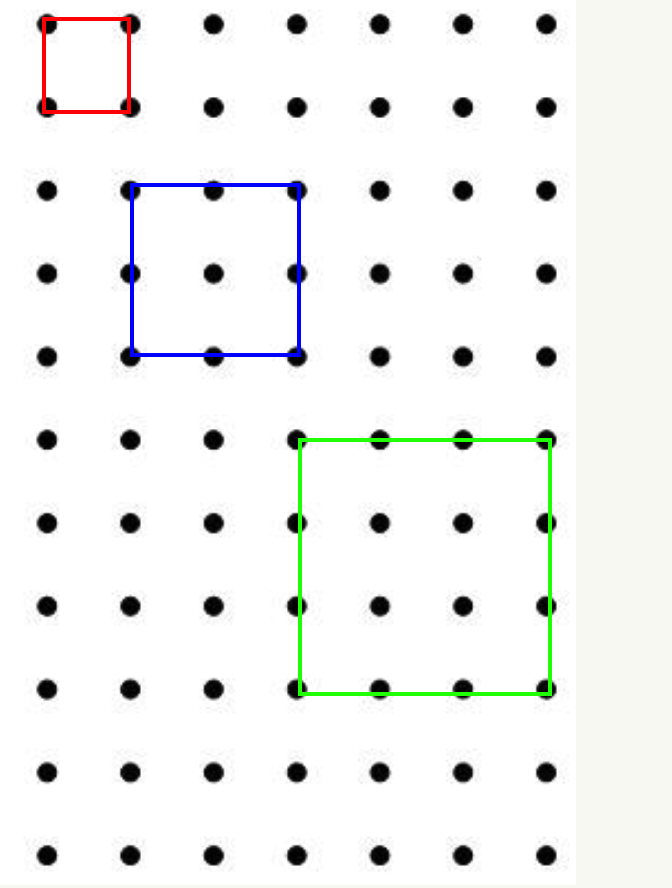
We can see that for a square of side 'a', the area is

and the number of grid points it covers, which is the number of flags you need, is

For the semicircles, we'll do an approximation, based on their area. We'll assume that since the grid has the same density of points everywhere, a circle of area 'a' will also require approximately flags. If our heart's square has side 'a', the radius of the semicircle is a/2, and the area of the two semicircle together is $\pi\cdot(a/2)^2$ or $\pi \frac{a^2}{4}$ , so we will need $\frac{(a+1)^2\cdot\pi\frac{a^2}{4}}{a^2}$ flags. After simplifying we get $(a+1)^2\pi/4$ . For the purpose of simplicity in our calculations, we'll round off the number of grid points from 2,997 to 3,000, and in total the number of grid points for both the square and the two semicircles is $(a+1)^2(1+\pi/4)=3000$ .