When we introduced the topic of tangent lines we said that the tangent is perpendicular to the radius, but did not prove this. This is an important property that is used in almost every geometry problem that involves circles and a tangent line. Here we will prove that the tangent is perpendicular to the radius, at the point where it intersects the circle.
Problem
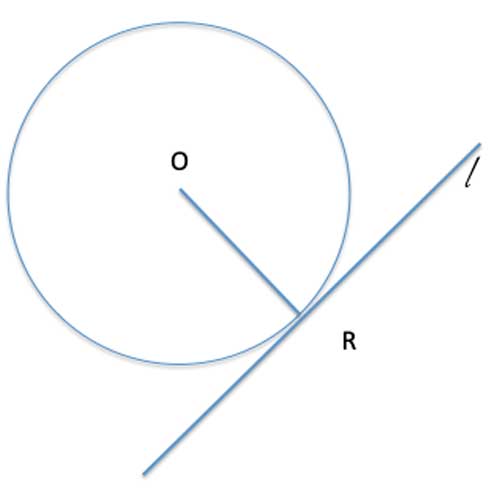
In circle O, l is a line tangent to the circle at point R. Prove that l⊥RO.
Strategy
Looking at the diagram, it just seems so obvious that it is true. In such cases, it is often useful to try and prove it is true using a proof by contradiction. We start by assuming that what seems to be true is false, and try to arrive at a contradiction.
A contradiction is when something impossible happens, which means our assumption is false. We assumed the opposite of what we need to prove, So if the assumption is false, it must be that what we needed to prove is true.
Let's see how this works out: We'll assume that l is not perpendicular to RO. Then there is another point on l, call it P, where OP is perpendicular to l. So triangle ΔOPR is a right triangle, with angle m∠OPR = 90°.
This means OR is the hypotenuse of that triangle, so it is the longest side of the triangle, OR>OP. Now, recall that a circle is a collection of all the points that are an equal distance - the radius- from the center of the circle.
Any point inside the circle is closer to the center than this distance, and any point outside the circle is farther than this. R is a point on the circle, and P is a point outside the circle, so OP>OR, and we have our contradiction. Our assumption that OR is not perpendicular to l is incorrect, and so we prove that the tangent is perpendicular to the radius, l⊥RO.