The HL theorem (with HL standing for Hypotenuse-Leg) is sometimes used to describe a fifth postulate for proving that triangles are congruent, in addition to the 4 basic ones (Side-Side-Side, Side-Angle-Side, Angle-Side-Angle, and Angle-Angle-Side).
The HL theorem only applies to right triangles, as the 'hypotenuse' specification implies. So to use it we need (1) a right angle, (2) a congruent side which is opposite that right angle - the hypotenuse, and (3) one of the other two sides.
We have already proven this theorem, using Pythagorean theorem. But here, we'll prove the HL theorem a different way, which does not rely on the advanced concept of Pythagorean theorem.
Problem
Two right triangles, ΔABC and ΔDEF have an equal hypotenuse (|AC|=|DF|) and an equal leg (|BC|=|EF|). Prove that the triangles are congruent.
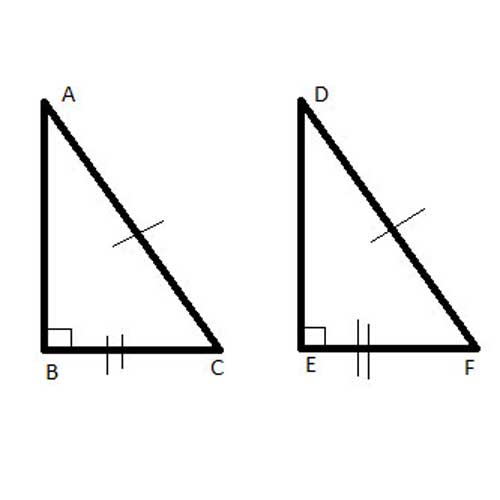
Strategy
We already have a couple of congruent sides, and a congruent angle, so we'll try to see if we can use one of the other 3 congruent postulates, by constructing another congruent side or angle.
Let's take triangle ΔABC, extend edge AB with a straight edge, and using a compass, construct a point G so that |BG|=|DE|.
To make it easier to see what we are doing, let's color-code the congruent sides:
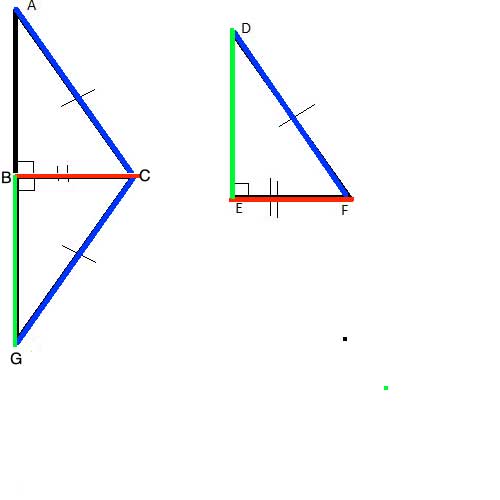
Now, consider triangles ΔDEF and ΔGBC: |BG|=|DE| by construction (the green leg), and |BC|=|EF|, as given in the problem formulation (the red leg).
∠CBG is a right angle, since it forms a linear pair with ∠CBA, which is a right angle as given in the problem. So m∠CBG = m∠DEF = 90° and ΔDEF ≅ ΔGBC by the Side-Angle-Side postulate.
If ΔDEF ≅ ΔGBC, then |CG|=|DF|, as corresponding sides of congruent triangles, and since |AC|=|DF| (given), |CG|=|AC| (transitive property of equality), making ΔACG an isosceles triangle. We have shown that in an isosceles triangle, the height to the base is also the median, so |AB|=|BG|. But |BG|=|DE| as corresponding sides in congruent triangles (ΔDEF ≅ ΔGBC), so |AB|=|DE| and we now have our third congruent side , and (ΔDEF ≅ ΔABC) by Side-Side-Side.
Proof
(1) |AC|=|DF| //Given
(2) |BC|=|EF| //Given
(3) m∠CBA =90° //Given
(4) m∠DEF =90° //Given
(5) |BG|=|DE| //Construction
(6) m∠CBG = m∠DEF = 90° //(3), ∠CBG and ∠CBA are a linear pair
(7) ΔDEF ≅ ΔGBC //(2), (5), (6), Side-Angle-Side
(8) |CG|=|DF| // corresponding sides of congruent triangles (CPCTC)
(9) |AC|=|DF| =|CG| //(1) , (8)
(10) |AC|=|CG| //(9) , transitive property of equality
(11) |AB|=|BG| //(10), ΔACG an isosceles triangle, (6) height to base of isosceles triangle is the median
(12) |AB|=|DE| //(11), (5) transitive property of equality
(13) ΔDEF ≅ ΔABC //(2), (1), (12), Side-Side-Side
