It is common to see geometry word problems related to the perimeter of geometric shapes. These problems attempt to connect the concept of perimeter to real-life problems. Here is one such example.
Problem
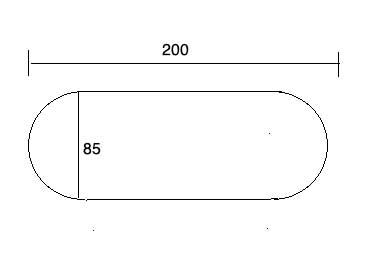
A hockey rink needs to have side-boards placed around the rink. The boarding costs $20/foot. The rink is made up of 2 semicircles at the ends of a rectangle as in this drawing. How much will it cost to install the side-boards?
Strategy
Working backward, the cost to install the boards is the length of boarding required. Which is the perimeter of the rink, multiplied by the cost per foot.
So we need to find the perimeter of the rink. The rink is made up of a rectangle, with two semi-circles. We will need to board both semi-circles, but only two sides of the rectangle (since the other two sides are interior to the rink, and surrounded by the semi-circles).
Finding the perimeter of two semi-circles is like finding the circumference of the full circle. Imagine we removed the rectangular part and pushed the two semi-circles together - we will have a full circle, which needs to be boarded around.
To find the circumference of a circle, we need its radius or diameter- and the diameter is given in the problem as 85, so the circumference is C= d*π=85π .
Now for the rectangle. We know the rink is 200 feet long, end to end, and this includes the two semi-circles. So the length of the straight part of the rink (the length of the rectangle) is 200 minus the diameter of the circle, 200-85=115. We have two such sides, so we will need to board 2*115 feet.
Solution
C= d*π=85π feet
Length of straight part = 200-85=115 feet
Perimeter of rink = 85π +2*115 = 85π+230
Cost to place boards: Perimeter * $20/foot = (85π+230) *20 = $9940.71 (rounded to nearest cent)
In conclusion, we've seen an example of how to solve a word problem related to the perimeter of geometric shapes.