Inscribed Shapes: Opposing Angles of a Quadrangle Inscribed in a Circle

In today's lesson, we will prove that in a quadrangle inscribed in a circle, the opposing angles are supplementary.

Not all quadrangles can be inscribed in a circle. Intuitively, if we think of a quadrangle like this slim diamond -

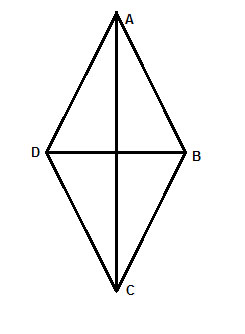
We can see that no circle can be drawn so that all four of its corners will be on the perimeter of that circle. If the top and bottom corners are on the circle, it will be too wide for the middle corners.

Conversely, we can think of a kite where one of the unequal angles is wide, and the opposing angle is narrow, and it seems possible that such a kite can be inscribed.

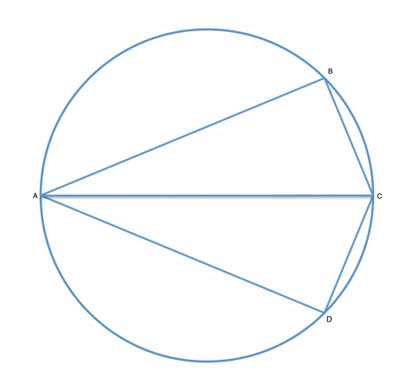
So which quadrangles can be inscribed? Those with opposing angles that are supplementary, as we will now prove.

Problem

Show that in a quadrilateral inscribed in a circle, the opposing angles are supplementary.

Show that m∠ABC + m∠CDA= 180°  and that  m∠BCD+ m∠BAD = 180°

Strategy

In previous problems, we have used different methods to show that angles are supplementary. When we had parallel lines, we used the consecutive interior angles theorem. When we had intersecting lines, we used angles that form a linear pair.

But here, we have none of those, so we will need to rely on something else. When dealing with circles and their angles, it is always useful to remember that a full circle measures 360°, and 360° is 180°x2.

Ah, now we are getting somewhere! An inscribed polygon has a set of inscribed angles, and we know from the Inscribed Angle Theorem that the inscribed angle's measure is half the arc that the inscribed angle subtends.

Since the opposing angles of the quadrilateral subtend two arcs that complement each other for a full circle, they must equal half of a full circle's measure in degrees- 180°.

Proof

Arc_BCD+Arc_DAB = 360°                                          //Two arcs that make up a full circle, measure 360°
Arc_ABC+Arc_CDA = 360°                                          //Two arcs that make up a full circle, measure 360°
m∠BCD+ m∠DAB = ½ (Arc_BCD+Arc_DAB) = 180°  // Inscribed Angle Theorem
m∠ABC+ m∠CDA = ½ (Arc_BCD+Arc_DAB) = 180°  // Inscribed Angle Theorem

And so we have proven that in a quadrangle inscribed in a circle, the opposing angles are supplementary.