Prove the Pythagorean Theorem Using Triangle Similarity

When we introduced the Pythagorean theorem, we proved it in a manner very similar to the way Pythagoras originally proved it, using geometric shifting and rearrangement of 4 identical copies of a right triangle.

Having covered the concept of similar triangles and learning the relationship between their sides, we can now prove the Pythagorean theorem another way, using triangle similarity.

Problem

In a right triangle ΔABC with legs a and b, and a hypotenuse c, show that the following relationship holds:

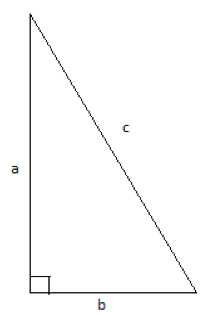
c^{2 =} a²+b²

Strategy

We said we would prove this using triangle similarity, so we need to create similar triangles. We have a right triangle, so an easy way to create another right triangle is by drawing a perpendicular line from the vertex to the hypotenuse:

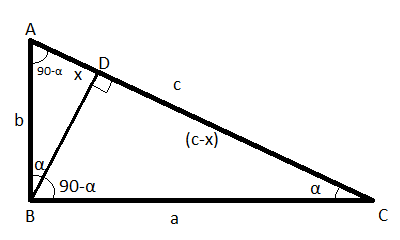
Observe that we created two new triangles, and all three triangles (the original one, and the two new ones we created by drawing the perpendicular to the hypotenuse) are similar. Why?

All three have one right angle (In the original triangle: ∠ABC. In the two new triangles: ∠BDA and ∠BDC).

Because the two new triangles each share an angle with the original one, their third angle must be (90°-the shared angle), so all three have an  angle we will call α (In the original triangle: ∠BCA. In the two new triangles: ∠BCD  and ∠ABD), and an angle which is 90°-α (In the original triangle : ∠BAC. In the two new triangles: ∠DBC  and ∠BAD).
So all three triangles are similar, using Angle-Angle-Angle.

And we can now use the relationship between sides in similar triangles, to algebraically prove the Pythagorean Theorem.

Proof

(1) m∠ABC=90°                                 //Given,  ΔABC is a right triangle
(2) m∠BDA = m∠BDC=90°               // BD was constructed as a perpendicular line to AC
(3) ∠ABC≅∠BDA ≅∠BDC                //(1), (2) transitive property of equality
(4) ∠BCA ≅ ∠BCD                             // Common angle, the reflexive property of equality
(5) m∠BAC = 90° - α                         // sum of angles in ΔABC is 180°, (1)
(6) m∠DBC = m ∠BAD  = 90° - α      // sum of angles in ΔDBC and ΔBAD is 180°, (2)
(7) ∠BCA ≅ ∠BCD ≅ ∠ABD             // (4), (6) sum of angles in a triangle
(8) ∠BAC≅∠DBC ≅ ∠BAD               // (5), (6)
(9) ΔABC ∼ ΔADB ∼ ΔBDC             // Angle-Angle-Angle
(10) a/c = (c-x)/a                              // Similar triangles - the long leg divided by the hypotenuse
(11) a² = c*(c-x)  = c² - cx                // cross multiply (10)
(12) c/b = b/x                                    // Similar triangles - hypotenuse divided by the short leg
(13) b² =  cx                                     // cross multiply (12)
(14) a² + b²= c² - cx + cx                //add (11), (13)
(15) a² + b²= c² // simplify (14)