We will solve most problems involving polygons inscribed in a circle by using theorems related to inscribed angles, as the vertices of the polygons form inscribed angles.
Problem
An irregular polygon ABCDE is inscribed in a circle of radius 10. Find the length of the arc DCB, given that m∠DCB =60°.
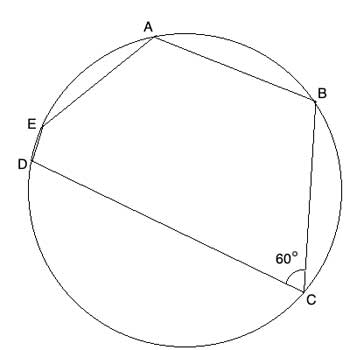
Strategy
Sometimes a problem involving inscribed shapes features regular polygons or other special shapes like a right triangle or an isosceles triangle. In those cases, we will try to make use of the unique features of those particular shapes.
But what if we are dealing with irregular polygons, like in this case? Then all we have to go by is the general characteristics of circles and their angles.
Since the polygon is inscribed in the circle, of special interest are the inscribed angles, which are the vertices of the polygon that lay on the circle's circumference.
We know that we can compute the length of the arc from the central angle that subtends the same arc. For an arc measuring θ°, the arc length s, is s= 2*π*r*θ°/360°. So we need to know the radius and the central angle.
Here, we have the radius -it is 10. We don't know the central angle. But we are given the measure of the inscribed angle that subtends the same arc (DAB). And we know the relationship between those two angles, which is given by the inscribed angle theorem.
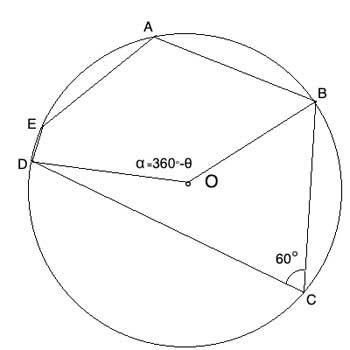
Finally, the arc whose length we are looking for (DCB) subtends a central angle (∠DOB) which complements the central angle of the arc DCB (that is, we need the other part of the circle). So it measures 360°-m∠DOB.
Solution
sArc= 2*π*r*θ/360°
r= 10 //From problem statement
m∠DCB =60° //From problem statement
m∠DOB = m∠α = 120° //Inscribed angle theorem
θ = 360°-α //complements α, for full circle
θ = 360°-120°=240°
sdcb= 2*π*10*240°/360°=40π/3
