Square Inscribed in a Circle

In this post, we derive formulas for all the properties of a square - the length of its sides, its perimeter, area and length of diagonals, using just the the radius of the circle it is inscribed in.

Conversely, we can find the circle's radius, diameter, circumference and area using just the square's side.

Problem 1

Find formulas for the square's side length, diagonal length, perimeter and area, in terms of r, the circle's radius.

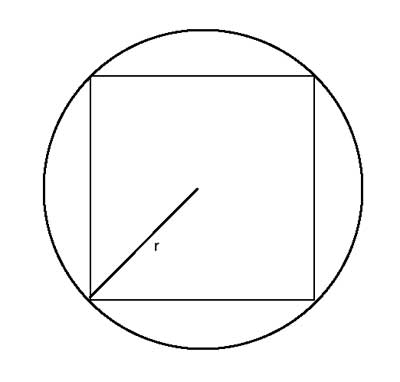
Strategy

The key insight to solve this problem is that the diagonal of the square is the diameter of the circle. We can show this using a symmetry argument - the square is symmetrical across its diagonal, so the diagonal must pass through the center of the circle.

Alternatively, we know that the square's interior angles are all right angles, which measure 90°. Since these angles are inscribed angles in a circle, they measure half of the central angle on the same arc. So the central angle measures 180°, which means it is the diameter.

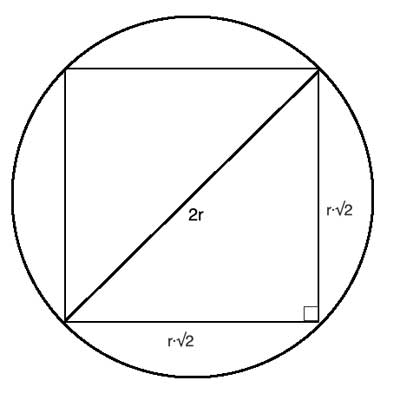
Armed with this knowledge, the length of the square's diagonal is simply 2r, each side measures r·√2 (Pythagorean theorem applied to a 45-45-90 triangle), the area is then 2r², and the perimeter is 4·r·√2.

Now let's do the converse, finding the circle's properties from the length of the side of an inscribed square.

Problem 2

Find formulas for the circle's radius, diameter, circumference and area, in terms of a, the side of the square.

Strategy

We already have the key insight from above - the diameter is the square's diagonal. We've already seen how to find the length of a square's diagonal from its side: it is a ·√2. The radius is half the diameter, so r=a·√2/2 or r=a/√2. The circumference is 2·r·π, so it is a·√2·π. And the area is π·r², so it is π·a²/2.

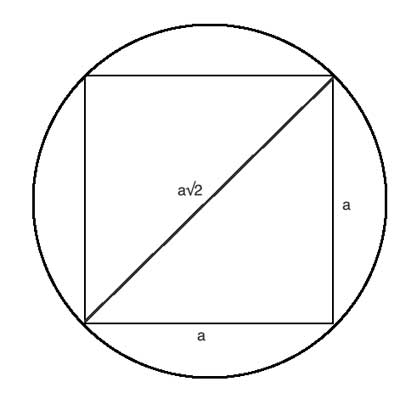
Now that we've done this, we can apply our knowledge to solve various kinds of "find the area of the shaded shape" problems related to a square inscribed in a circle, like this one:

Problem 3

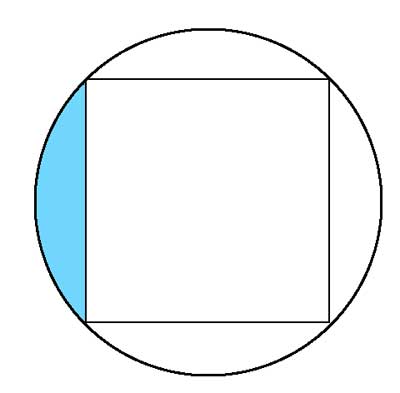
Find the area of the shaded shape, given the square's side is 'a'. Then, find it in terms of the circle's radius, 'r'.

Strategy

The strategy for finding the area of irregular shapes is usually to see if we can express that area as the difference between the areas formed by two or more regular shapes.

Here, it is very easy - the 4 irregular shapes are all the same size (from symmetry). The sum of their areas is the difference between the area of the circle and the area of the square.

So the shaded area is A_shaded=(A_circle-A_square)/4

If we have the side of the square, a, we get A_shaded=(A_circle-A_square)/4=(π·a²/2 -a²)/4=(π-2)·a²/8.

And if we have the radius, 'r', A_shaded=(A_circle-A_square)/4= (π·r²-2r²)/4=(π-2)·r²/4

Now that we've done that, we can solve a similar problem where we have a circle inscribed in a square.