A reader wanted some help and sent me the following problem, involving lines that intersect on a trapezoid's midsegment:
Problem:
EF is the midsegment of trapezoid ABCD, and the two line segments KM and LN intersect at point O, which lies on EF. Show that |KO|=|OM| and |NO|=|OL| .
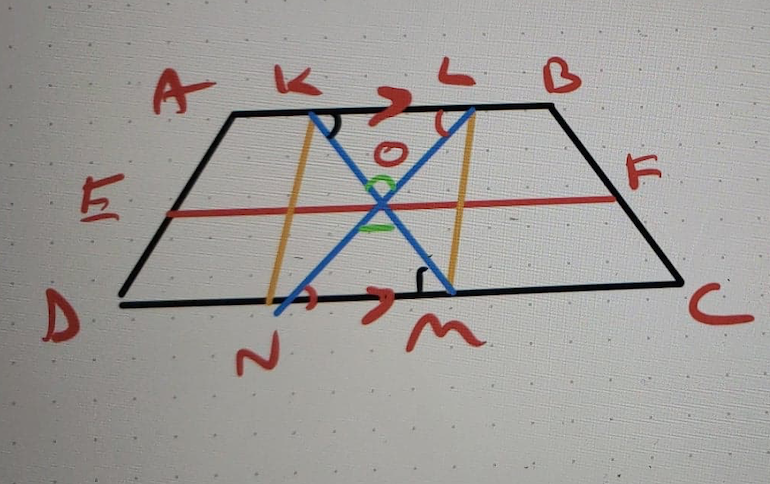
The original problem is quite easy to prove, using the converse trapezoid midsegment theorem, and we will prove a couple of additional things- |KN| =|LM|, and |KL|=|NM|.
Strategy
The problem statement begins with saying the EF is a midsegment in a trapezoid, so we will use the properties of such midsegments. As we have proven, the midsegment of a trapezoid is parallel to both of the bases. So EF is parallel to DC. Now let's look at the quadrilateral AKMD. It is also a trapezoid, since AK is just a sub-segment of AB and DM is a sub-segment of DC. As ABCD is a trapezoid, AB||CD, and so AK||DM, and since EF|| DC, it also follows that EF||DM.
Now we will use the converse trapezoid midsegment theorem , and apply it to trapezoid AKMD. The converse trapezoid midsegment theorem states that in a trapezoid, a line that intersects the midpoint of one of the legs and is parallel to one of the bases, it is a midsegment, and it intersects the other leg's midpoint. So in trapezoid AKMD, EF intersects the midpoint of leg AD, and is parallel to DM, making it a midsegment, and the result is that it intersects the other leg (KM) at its midpoint, proving that |KO|=|OM|.
We can repeat this entire process for the quadrilateral LBCN. LB is just a sub-segment of AB and CN is a sub-segment of DC. As ABCD is a trapezoid, AB||CD, and so LB||CN, and since EF|| DC, it also follows that EF||CN. Applying the converse trapezoid midsegment theorem to LBCN, EF intersects the midpoint of leg BC, and is parallel to CN, making it a midsegment, and the result is that it intersects the other leg (LN) at its midpoint, proving that |NO|=|OL|.
Additional proofs
So we have proven what was required in the original problem, now let's prove the additional things.
Consider triangles ΔOKN and ΔOML. We have just shown that |KO|=|OM| & |NO|=|OL|. ∠KON and ∠MOL are vertical angles, so they are congruent, and so ΔOKN ≅ ΔOML by the Side-Angle-Side postulate, and |KN| =|LM| as corresponding sides in congruent triangles.
Similarly, if we look at triangles ΔOKL and ΔOMN - we have just shown that |KO|=|OM| & |NO|=|OL|. ∠KOL and ∠MON are vertical angles, so they are congruent, and so ΔOKL≅ ΔOMN by the Side-Angle-Side postulate, and |KL|=|NM| as corresponding sides in congruent triangles.
This is an interesting result - in a trapezoid, any two lines that intersect at a point that lies on the trapezoid's midsegment, cut congruent segments from the trapezoid's bases.
Proof
(1) EF ||DC //Given, EF is the midsegment of trapezoid ABCD
(2) |AE|=|ED| //Given, EF is the midsegment of trapezoid ABCD
(3) AK||DM //Given, ABCD is a trapezoid, AK and DM are sub-segments of parallel lines
(4) |KO|=|OM| //Converse midsegment theorem in trapezoid AKMD
(5) |BF|=|FC| //Given, EF is the midsegment of trapezoid ABCD
(6) LB||CN //Given, ABCD is a trapezoid, LB and CN are sub-segments of parallel lines
(7) |NO|=|OL| //Converse midsegment theorem in trapezoid LBCN
(8) ∠KON ≅ ∠MOL //Vertical angles
(9) ΔOKN ≅ ΔOM //(4), (7), (8), Side-Angle-Side postulate
(10) |KN| =|LM| //Corresponding sides in congruent triangles (CPCTC)
(11)∠KOL ≅ ∠MON //Vertical angles
(12) ΔOKL≅ ΔOMN //(4), (7), (10), Side-Angle-Side postulate
(13) |KL|=|NM| //Corresponding sides in congruent triangles (CPCTC)
