A simple extension of the Inscribed Angle Theorem shows that the measure of the angle of intersecting chords in a circle is equal to half the sum of the measure of the two arcs that the angle and its opposite (or vertical) angle subtend on the circle's perimeter.
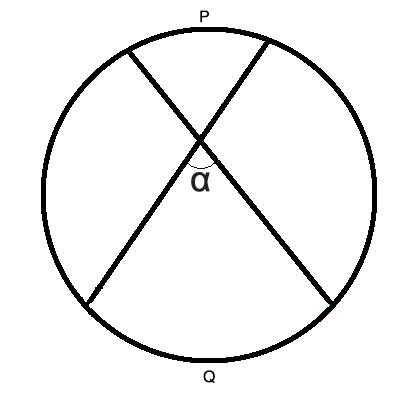
That is, in the drawing above, m∠α = ½(P+Q).
Problem
Show that the angles of Intersecting chords are equal to half the sum of the arcs that the angle and its opposite angle subtend, m∠α = ½(P+Q).
Strategy
We already know something about angles between chords, if those chords intersect on the circle's perimeter and form an inscribed angle. And interestingly, that angle is also equal to ½ of something - one half of the central angle or one half of the arc they subtend. This is a strong hint that our proof will need to use inscribed angles. So let's create such inscribed angles, by connecting the points where these chords intersect the circle:
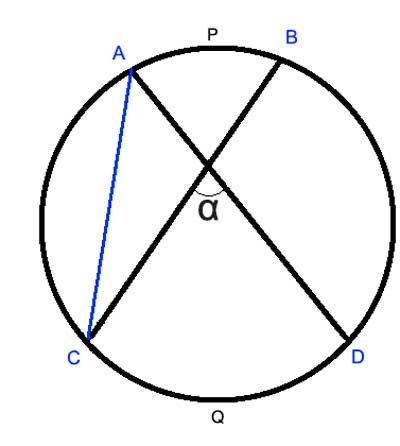
Now we have our inscribed angles, and by the Inscribed Angle Theorem we have m∠ACB=½P and m∠CAD=½Q, because the degree measure of the arcs P and Q is the same as the measure of the central angle that subtends them. And the inscribed angle is equal to half the central angle that subtends the arc.
But look at angle α - it is an exterior angle to the triangle formed by AC, CB and AD (ΔAαC). By the Triangle Exterior Angle Theorem, it is equal to the sum of the interior angles not adjacent to it.
m∠α =m∠ACB+m∠CAD=½P+½Q= ½(P+Q)
Proof
(1) m∠ACB=½P // Inscribed Angle Theorem
(2) m∠CAD=½Q // Inscribed Angle Theorem
(3) m∠α =m∠ACB+m∠CAD //Triangle Exterior Angle Theorem
(4) m∠α =½P+½Q= ½(P+Q) //Substitution, transitive property of equality
Some Variations
Sometimes you may see problems that use slight variations of this in the way the problem is posed. For example, find m∠x in this drawing:
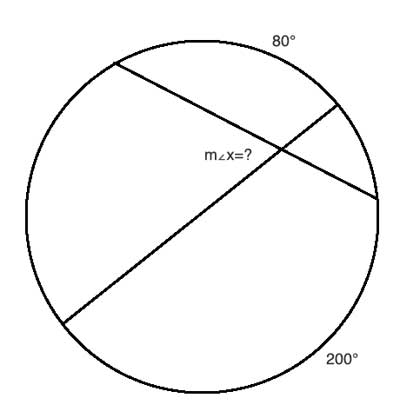
Here, we have two arcs whose measure is given, but x is not an angle formed by lines subtending those arcs. Instead, it is an angle that forms a linear pair with the angle formed by the chords lines subtending those arcs. So, the solution is simple - first, we'll find the measure of the angle that does subtend the given arcs. Using the above, it is ½(200°+80°) = 140°, and since x supplements it to form a linear pair, it is equal to 180°-140°, and m∠x=40°
Chords intersecting outside the Circle
Above we've shown that when two chords intersect inside the circle, the angle formed at their intersection point is equal to half the sum of the arcs they subtend. But what happens if the two chords intersect at a point outside the circle?
It turns out we can use a very similar strategy to come up with a simple formula for that angle, as well. Suppose we have two chords, BC and ED, that intersect at point A outside the circle, as in the drawing below.
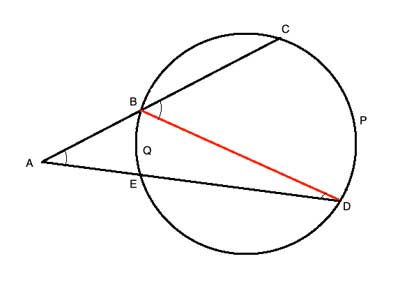
As before, we will create two inscribed angles by connecting the points where these chords intersect the circle with line BD. In the triangle ΔABD, ∠BAD is an interior angle, and so is one of the inscribed angles, ∠BDA. The other inscribed angle, ∠CBD, is now an exterior angle, and so it is equal to m∠BAD+m∠BDA. And since the inscribed angles are each equal to half the measure of the arc they subtend, we have
m∠CBD=m∠BAD+m∠BDA
m∠BAD = m∠CBD - m∠BDA
m∠BAD = ½P - ½Q =½(P-Q)
