Solving geometry word problems is often a challenge. The biggest one is how to translate the description of the problem from words into a graphical representation. In other words, how to visualize the problem. Here is an example, sent to me by a reader who was having difficulty with this very issue of visualization.
Problem
A malfunction occurred in a nuclear power-plant. Following the malfunction, the area of the plant, measuring a square kilometer, was contaminated with radioactive waste. Because of the radiation, no one can live within one kilometer of any point within the contaminated area. Find the total area that has become uninhabitable, including the interior of the square.
Strategy
The first step in solving geometry word problems is to translate the description into a graphical representation of the problem. Sometimes, we face a challenge in that the description itself is a bit ambiguous. In those cases, we need to make assumptions. Whenever we do so, we should note what assumptions we are making.
So, for example, in the above problem, we are told that the area of the plant measures a square kilometer - but we are not explicitly told its shape until the last sentence that says, "including the interior of the square". If we did not have that last sentence, we would not know the shape of the plant area- it could be a circle with an area of 1 square kilometer, or a square with a side measuring 1 km, or it could be just a random shape. So we would make an assumption " I assume the plant area was a square" or " assume the plant was a circle", and solve based on the assumption.
So here, we have a square-shaped plant with an area of 1 square kilometer. From the formula for an area of a square , Asquare=side2, we get 1=side2, so each side measures 1 Km:

Step 1
Now, let's figure out what other areas are within one kilometer of any point within the this area.
The strategy here is to look at the square's edges - because every point inside the square is going to be farther away from a point outside the square then the edge:
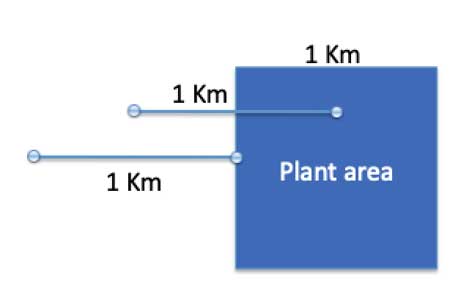
So the farthest point from each side of the square that is still within 1 km of it, is a point that is 1 km from the edge. Now, if we recall that Parallel lines are equidistant from each other, we can draw a parallel line measuring one kilometer in length, 1 Km away from the edge of the square, and all points between that parallel line and the edge of the square will be within 1 Km of the square, and thus also part of the uninhabitable area. It is easy to see that this forms another square, also measuring 1 square kilometer, constructed on the edge of the original square:
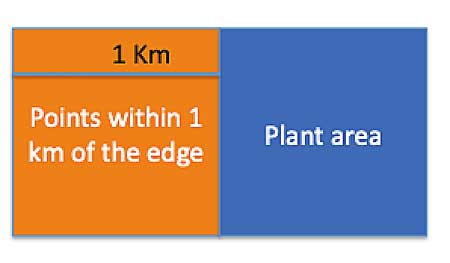
Step 2
But we have 4 such squares, one on each edge of the original plant site:

So , a total of 5 squares, each measuring 1 square kilometer.
Step 3
So we've made some progress solving this problem. But that's not all. What about the space between the squares? There are points in that space that are also within 1 kilometer of the original square - any point that is less than 1 kilometer from the corner. We know that a circle is defined as the collection of all points that are the same distance from one point, which is the center of the circle. We can think of that corner of the square as the center of a circle with radius 1 Km.
Then, we have between each of the squares we constructed on the side of the original plant, a quarter of a circle. Within that quarter-circle, all the points are within 1 Km of the corner. They, too, are part of the uninhabitable area:
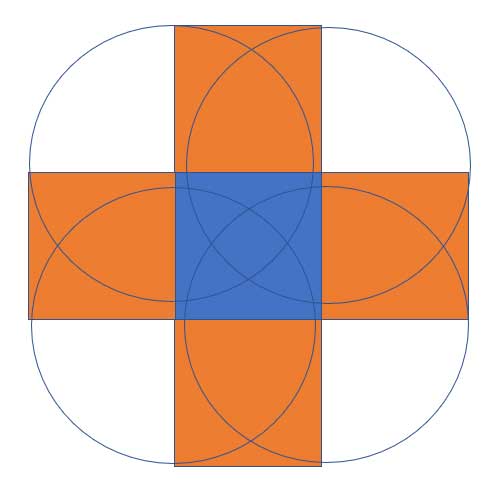
So now we have translated this problem into a simple graphical representation. All that remains are a few simple calculations.
There are four such quarter-circles, and they are identical. The total area of them is the area of one full circle with radius 1: Acircle=π*r2 , with r=1, so the area is just π.
So, the solution to this problem is now to sum it all up. The total uninhabitable area is: 1(original square)+ 4x1(squares on each edge) + π = 5+π square kilometers have become uninhabited.
