The harmonic mean is a kind of an average. For two values, a and b, it is defined as H= 2ab/(a+b). So what's the harmonic mean in a trapezoid? We have already seen several lines that are parallel to the bases of the trapezoid that are also a kind of an average.
The trapezoid mid-segment is the arithmetic mean , or average, of the two bases. If the bases are a and b, the midsegment's length, M, is equal to M=(a+b)/2. We also saw that the parallel line that splits the trapezoid into two similar trapezoids is the geometric mean of the bases, M=√(ab). And the area bisector which partitions the trapezoid into two smaller trapezoids with equal areas is the quadratic mean (or Root Mean Square – RMS) of the two bases, M= √[(b2+a2)/2].
So, is there also such a special line, parallel to the bases, which is the harmonic mean in a trapezoid? Turns out, there is. It is the parallel line through the point of intersection of the trapezoid's diagonals, as we will show in this problem.
Problem
In trapezoid ABCD, where AB||CD, the two diagonals intersect at point E. Show that a line parallel to the bases and passing through E is the harmonic mean of the trapezoid. That is, show that |FG|= 2ab/(a+b)
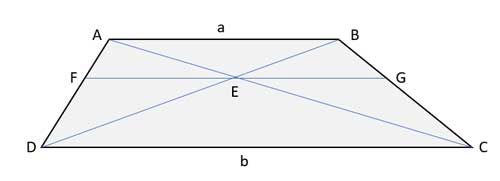
Strategy
There are a couple of hints in the problem that point us to using similar triangles in the proof. The first is that with the diagonals, we have so many similar triangles, as we saw when we looked at the ratio of the area of triangles created by the diagonals in a trapezoid.
The second hint is that we are being asked to show a leadership between line segments that is a ratio. We've already seen several problems that require finding the ratio of line segments, which rely on using similar triangles. They all make use of the fact that if ΔABC∼ ΔDEF, then AB/DE=BC/EF=AC/DF. That is the scale factor.
So let's try to do this thing with similar triangles, using the same pair we used when we discussed the Ratio of Area of Triangles in a Trapezoid, ΔABE and ΔCDE. We have two congruent angles that are alternating interior angles between parallel lines. And we have one pair of vertical angles, so the two triangles are similar. The scale factor is a/b. Let's label the other corresponding sides as 'x' and 'y', and 'z' and 'w', and their ratios, x/y and z/w is also equal to the scale factor a/b.
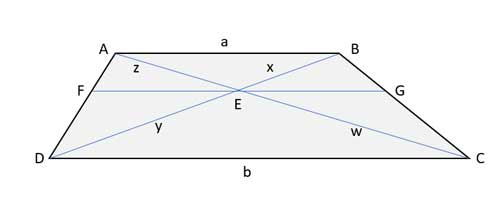
Adding in the line FG
Ok, so how does the line FG fit into all this? FG is made up of two segments, FE and EG. Each of those segment is parallel to the bases of the trapezoid, creating two pairs of similar triangles- ΔCEG∼ ΔCAB and ΔDEF∼ ΔDBA. In both pairs, the similar triangles share a common apex angle, and the other two pairs of angles are corresponding angles of parallel lines.
So from this similarity we have in triangles ΔCEG∼ ΔCAB, |EG|/a = w/(z+w). Rearranging, we get |EG|=a⋅w/(z+w). Let's divide the numerator and denominator by w: |EG|=a/(z/w+1). And from the above, we know that z/w=a/b, so |EG|=a/(a/b+1)=a/[(a+b)/b]=ab/(a+b)
In the same way, in triangles ΔDEF∼ ΔDB , |EF|/a = y/(y+x). Rearranging, we get |EF|=a⋅y/(y+x). Let's divide the numerator and denominator by y: |EF|=a/(x/y+1). And from the above, we know that x/y=a/b, so |EF|=a/(a/b+1)=a/[(a+b)/b]=ab/(a+b)
Combining these two parts: |FG|=|EG|+|EF|= ab/(a+b) + ab/(a+b) = 2ab/(a+b), as required, and FG is indeed the harmonic mean of the trapezoid's two bases.
Proof
(1) AB||CD //Given
(2) ∠ACD≅ ∠CAB //Alternating interior angles between two parallel lines
(3) ∠ABD ≅ ∠BDC //Alternating interior angles between two parallel lines
(4) ∠BEA ≅ ∠DEC //Vertical angles
(5) ΔABE∼ ΔCDE //(2), (3), (4), Angle-Angle-Angle
(6) a/b=x/y=z/w //(5) The scale factor of corresponding sides in similar triangles is the same
(7) ∠ECG ≅ ∠ACB //common angle
(8) ∠EGC≅ ∠ABC //Corresponding angles between two parallel lines
(9) ∠GEC ≅ ∠BAC //Corresponding angles between two parallel lines
(10) ΔCEG∼ ΔCAB //(7), (8), (9), Angle-Angle-Angle
(11) ∠EDF ≅ ∠BDA //common angle
(12) ∠EFD ≅ ∠BAD//Corresponding angles between two parallel lines
(13) ∠FED ≅ ∠ABD //Corresponding angles between two parallel lines
(14) ΔDEF∼ ΔDB //(11), (12), (13), Angle-Angle-Angle
(15) |EG|/a = w/(z+w) //(10) , scale factor of similar triangles
(16) |EG|=a⋅w/(z+w) = a/(z/w+1) //rearrange and divide by w
(17) |EG|=a/(a/b+1)=a/[(a+b)/b]=ab/(a+b) //(16) , (6)
(18) |EF|/a = y/(y+x) //(14) , scale factor of similar triangles
(19) |EF|=a⋅y/(y+x)) = a/a/(x/y+1) //rearrange and divide by y
(20) |EF|=a/(a/b+1)=a/[(a+b)/b]=ab/(a+b) //(19) , (6)
(21) |FG|=|EG|+|EF|= ab/(a+b) + ab/(a+b) = 2ab/(a+b) //(17) , (20)
