In another problem, we saw that in an isosceles triangle, the height to the base from the apex is also the angle bisector. Here, we will show the opposite: that the angle bisector is perpendicular to the base in an isosceles triangle. This means the angle bisector is also the height to the base.
Problem
Triangle ΔABC is isosceles, |AB|=|AC|. AD bisects the angle ∠CAB. Show that AD is perpendicular to BC: AD⊥BC
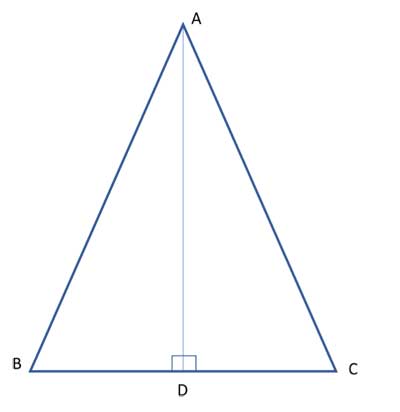
Strategy
In this proof, and in all similar problems related to the properties of an isosceles triangle, we employ the same basic strategy. we use congruent triangles to show that two parts are equal. Since this is an isosceles triangle, by definition we have two equal sides.
And using the base angles theorem, we also have two congruent angles. We then take the given line – in this case, the apex angle bisector – as a common side, and use one additional property or given fact to show that the triangles formed by this line are congruent.
Here, the additional given fact is that the line is an angle bisector, so ∠DAC ≅ ∠DAB, and from here it easily follows that ΔDAC is congruent to ΔDAB, using the Side-Angle-Side postulate. From this, we get that ∠BDA≅∠CDA as corresponding angles in congruent triangles. And since ∠BDA and ∠CDA form a linear pair, they must both be equal, and each measure 90°, proving that the angle bisector is perpendicular to the base in an isosceles triangle.
Proof that the angle bisector is perpendicular to the base in an isosceles triangle
- |AB|=|AC| //Given
- |AD|=|AD| //Common side , reflexive property of equality
- ∠ DAC = ∠DAB //Given, AD is the angle bisector
- DAC ≅ DAB //(1), (2), (3), Side-Angle-Side postulate
- ∠BDA≅∠CDA //(4) corresponding angles in congruent triangles CPCTC)
- m∠BDA=m∠CDA=90° //(5), linear pair theorem
- AD⊥ BC //(6) definition of perpendicular lines