In today's lesson, we will prove the Angle Bisector Equidistant Theorem.
When two rays intersect at a point, they create an angle, and the rays form the two sides of this angle. A line that splits this angle into two equal angles is called the angle bisector.
The Angle Bisector Equidistant Theorem state that any point that is on the angle bisector is an equal distance ("equidistant") from the two sides of the angle.
The converse of this is also true. If a point lies on the interior of an angle and is equidistant from the sides of the angle, then a line from the angle's vertex through the point bisects the angle.
Problem
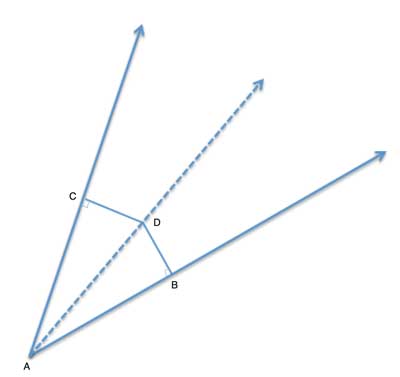
AD is the angle bisector of angle ∠BAC (∠BAD≅ ∠CAD). Show that for any point D, the perpendicular distances |DC| and |DB| are equal.
Strategy
This is a simple proof using congruent triangles - which is the strategy of first choice when we need to show that two things are equal. In this case, to show that the distance between the point on the bisector and the two sides of the angel is equal.
The triangles are already present in the problem's drawing - △ABD and △ACD. They share a common side (AD).
One of their angle pairs is a right angle (as that is the definition of distance) and the other pair of angles is equal since AD is the bisector - and we can show the triangles are congruent using the Angle-Side-Angle postulate.
Proof
(1) AD=AD //Common side, reflexive property of equality
(2) ∠BAD≅ ∠CAD //Given, AD is the angle bisector of ∠BAC
(3) m∠DCA=m∠DBA=90° //definition of distance.
(4) ∠ADC≅ ∠ADB //(2),(3), Sum of angles in a triangle
(5)△ABD≅△ACD //(2),(3),(4), Angle-Side-Angle Postulate
(6) |DB|=|DC| //Corresponding sides of congruent triangles (CPCTC)