In today's lesson, we will learn a step-by-step proof of the Converse Perpendicular Transversal Theorem: If two lines are perpendicular to a 3rd line, then they are parallel to each other.
In the previous problem, we showed that if a transversal line is perpendicular to one of two parallel lines, it is also perpendicular to the other parallel line.
Now we will show the opposite - that if a transversal line is perpendicular to two lines, then those two lines are parallel.
Prove:
If two lines are both perpendicular to one other line, then they are parallel to each other.
Given:
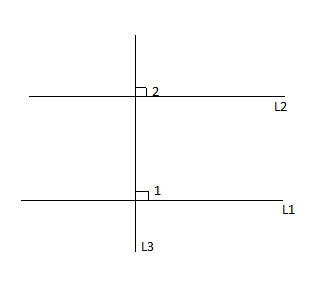
L3 ⊥ L1, L3 ⊥ L2, prove L1 || L2
Proof
(1) L3 ⊥ L1 //given
(2) m∠1 = 90° //from (1) definition of perpendicular lines
(3) L3 ⊥ L2 //given
(4) m∠2 = 90° //from (1) definition of perpendicular lines
(5) m∠1 = m∠2 // transitive property of equality, both equal 90°
(6) ∠1 ≅ ∠2 //from (5) and definition of congruency
L1 || L2 //two lines are parallel if the corresponding angles formed by a transversal line are congruent
Strategy for this problem:
To show that two lines are parallel, we typically need to find two corresponding angles that are equal. The corresponding angles here are ∠1 ND ∠2, and using the facts given in the problem - that these are both right angles (since both L1 and L2 lines are perpendicular to L3), they are equal.
And that's how we prove the Converse Perpendicular Transversal Theorem.