In today's lesson, we will see a step by step proof of the Perpendicular Transversal Theorem: if a line is perpendicular to 1 of 2 parallel lines, it's also perpendicular to the other.
In the section that deals with parallel lines, we talked about two parallel lines intersected by a third line, called a "transversal line".
The transversal line can intersect the parallel lines at any angle. When the angle of intersection is a right angle (90°), the transversal line is called a "perpendicular transversal", and we will now show that if it is perpendicular to one line, it is also perpendicular to the other parallel line.
Prove:
If a line is perpendicular to one of two parallel lines, then it is also perpendicular to the other one.
Given:
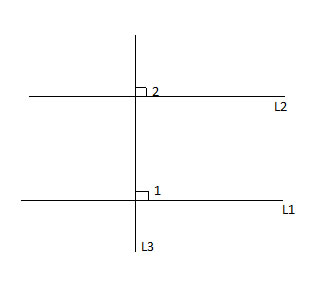
L3 ⊥ L1, L1 || L2, prove L3 ⊥ L2
Proof
Here's how you prove the Perpendicular Transversal Theorem:
(1) L3 ⊥ L1 // given
(2) m∠1 = 90° // definition of perpendicular lines
(3) L1 || L2 // given
(4) m∠1 = m∠2 // corresponding angles of two parallel lines
(5) m∠2 = 90° //from (2) & (4) , using algebraic substitution
(6) L3 ⊥ L2 // definition of perpendicular lines
Strategy for this problem:
Like almost any problem involving parallel lines, we will prove this by finding corresponding angles. And, like any other proof problem, we will be making use of all the information given in the problem statement.
So, we were given the fact that L1 and L2 are parallel - so we use that and see the corresponding angles (∠1 and ∠2 ) - which we know are equal. We were also given the fact that m∠1 = 90° since L3 and L1 are perpendicular lines. So, using both facts we have m∠1 = m∠2= 90°, and we are done.
