In this problem, we have two circles inscribed in a square, with their centers on the square's diagonal. The circles are tangent to each other, and tangent to the square's sides. We are given only their radius, which is 1 unit. How can find the square's side length, using only this information?
Strategy
So, we have two circles inscribed in a square, and most geometry problems involving inscribed circles and squares make use of tangent lines. Remember, a circle's radius is perpendicular to the tangent line at the point of tangency. We'll use that in this problem. The other key to solving this is to observe that the circles' centers are on the square's diagonal, and use the properties of a square's diagonal. One such property is that the diagonals of a square bisect the square's angles.
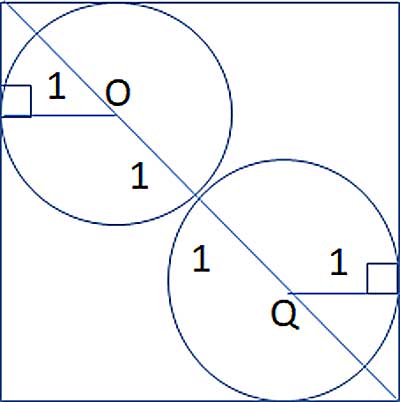
We'll use this property to solve this problem in two slightly different ways.
First Way for Solving this Problem
Let's draw the square's diagonal, and radii to where the circles touch the square's sides:
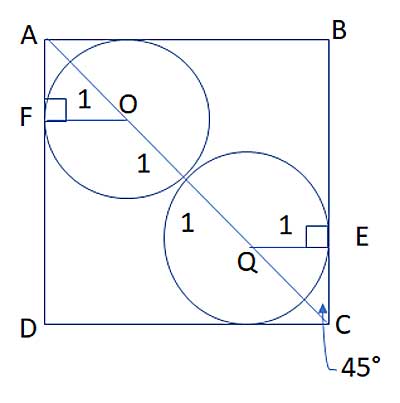
The square's diagonal, AC, bisects the angle ∠DCB, so angle ∠QCE measures 45°. The radius QE is perpendicular to the side CB at the point of tangency, E. This means triangle ΔQEC is a 45-45-90 right triangle, so QC=√2.
In a similar manner, we can show that QC=√2,
OQ, the part of the diagonal between the two centers is equal to 2, as it is made up of two radii, each measuring 1.
Putting these together, the whole diagonal is AC=AO+OQ+QC=√2+2+√2= 2+2√2.
The relationship between the square's diagonal (d) and its side (a) is d=a√2. So taking the above and solving for a we get a=d/√2 = (2+2√2)/√2=2/√2 + 2√2/√2=√2+2
Second way
Now, suppose you didn't immediately see that you can first find the square's diagonal and then find the length of the side for the diagonal. Let's solve this a second way. Let's draw a line, GH, parallel to the square's sides and through one of the circle's center:
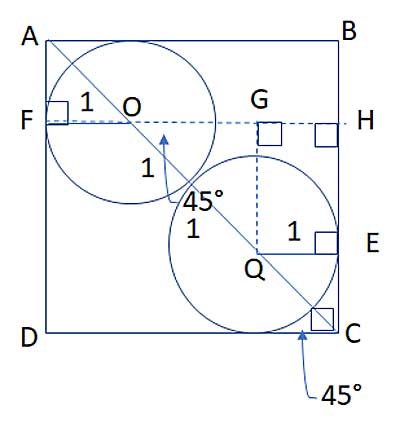
Note that the side is made up of the following 3 segments: FO, OG, and GH. FO is the radius of one of the circles, so it is equal to 1. GH was formed by drawing a perpendicular line from Q to FH, so it is parallel to CB (by the converse interior angles theorem). QE is perpendicular to CB, as the radius is perpendicular to the tangent, so QE||DC (also by the converse interior angles theorem). QGHE is thus a parallelogram (a rectangle, actually), and QE=GH. QE is also the radius of one of the circles, so it, too, is equal to 1.
That leaves OG. In triangle ΔGOQ, ∠OGQ=90° (QGHE is a rectangle).FH||DC (we constructed it that way) so ∠GOQ≅∠DCO as alternating interior angles, and so m∠GOQ=45°. Triangle ΔGOQ is thus a 45-45-90 right triangle, with a hypotenuse ( OQ) equal to 2, as it is made up of the two radii). Its side is 2/√2=√2. And so the side of the square, FO+OG+GH, is 1+√2+1=√2+2
