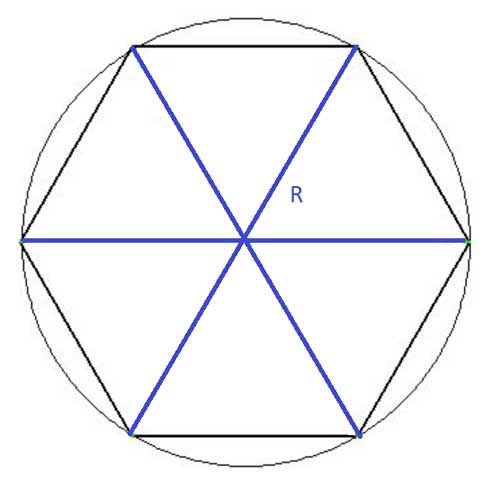
In this post, we'll take a closer look at a regular hexagon - a six-sided polygon where all the sides are equal. We will look at its angles, and find formulas for its perimeter and area using its side or radius.
Definition
A regular polygon is a two-dimensional convex shape whose sides and interior angles are all equal. A regular hexagon has six sides, which are all equal, and six equal interior angles.
Interior Angles
For any polygon, the sum of the interior angles is S=(n-2)•180°, where n is the number of sides of the polygon. In a hexagon, n=6, so the sum of the interior angles in a hexagon is (6-2)•180°=4•180°=720°. And since all the interior angles of a regular hexagon are equal, each one measures 720°/6=120°. From this we derive many other interesting properties, starting with showing that a regular hexagon is made up of 6 equilateral triangles.
Proof
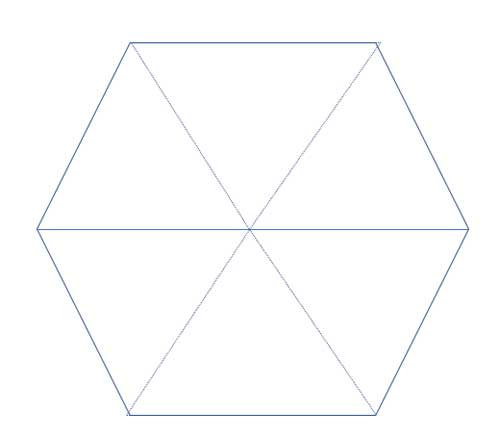
Many of the "proofs" I've seen that show that a regular hexagon is comprised of six equilateral triangles start with things like "Draw a circle that passes through the regular hexagon's vertices" - but they do not prove that you can actually draw such a circle (it's possible to do this, of course, but it is rather complex). So let's formally prove this intuitive result.
Let's draw the angle bisectors of two adjacent interior angles, and call their point of intersection O:

It is easy to see that ΔOAB is equilateral - m∠BAF = m∠ABC = 120°, as interior angles of a regular hexagon. The angle bisectors create two half angles which measure 60°: m∠OAB=m∠OBA=60°. And from the sum of angles in a triangle, ∠AOB is also a 60° angle, and ΔOAB is an equilateral triangle.
Now let's connect O with vertex C, and compare triangles ΔOAB and ΔOCB
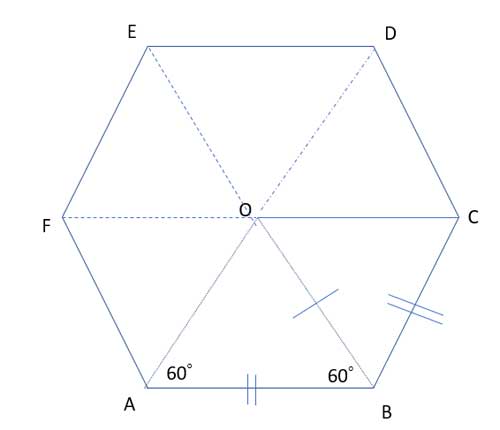
OB=OB as a common side
AB=BC as equal sides of a regular hexagon
m∠ABO=m∠CBO=60° as BO is the angle bisector
∠ABO≅∠CBO (definition of congruent angles)
So ΔOAB and ΔOCB are congruent triangles by the Side-Angle-Side postulate, and ΔOCB is an identical equilateral triangle to ΔOAB. We can continue and do this for the rest of the sides, connecting point O to vertices D, E and F, to arrive at the desired result - there are six identical equilateral triangles making up the hexagon, all meeting at its center, O.
Area and Perimeter
Since we have shown that six equilateral triangles make up a regular hexagon, it is easy to come up with a formula for its area - it is 6 times the area of one of the equilateral triangles. We have shown how to derive a formula for the area of an equilateral triangle from the length of its side: AreaΔequilateral=(s2*√3)/4, where s is the length of the side.
[A quick reminder of how we did this: If we take the height to the base of any of these triangles we will get a 30°-60°-90° right triangle, with a hypotenuse equal to s, a leg equal to s/2, and another leg equal to s/2·√3. The area of such a triangle is (leg · leg)/2, or (s/2 · s/2·√3)/2. Two identical 30-60-90 triangles make up the equilateral triangle, so its area is 2*(s/2 * s/2·√3)/2=(s2*√3)/4]
So Area⬡hex=6•(s2*√3)/4=3•√3•s2/2.
The perimeter of any polygon is simply the sum of its its sides. In a regular hexagon, all sides are equal, so P⬡hex=6s.
Radius
The radius of a regular polygon is the distance from its center to any one of its vertices. From symmetry, this distance is equal for all vertices. So what is this radius in a regular hexagon? We already saw that the center of the regular hexagon forms an equilateral triangle with the edges, so its radius (R) is equal to the length of each of the sides. This also shows we can inscribe a regular hexagon in a circle with radius R.