We are used to seeing the term 'radius' in the context of circles - the radius of the circle is the distance from its center to any point on its circumference.
But in geometry, we also use the term 'radius' for regular polygons - those where all the sides and interior angles are equal. The radius of a regular polygon is the distance from its center to any one of its vertices. From symmetry, this distance is equal for all vertices.
A square is a regular polygon with 4 sides, and its center is the point which is an equal distance from all four corners - so it is the midpoint of its diagonals, which are equal and bisect each other.
Let's look at an interesting geometry problem which involves the center of squares, using a property of squares constructed on the sides of triangles, we have proven earlier.
Problem
O and Q are the centers of squares ACGD and AEFB, respectively. M is the midpoint of CB (CM=MB). Prove that OM=QM and that OM⊥QM.
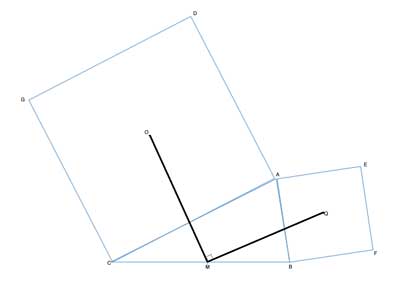
Strategy
As we did before, since we need to prove two things and splitting complex problems into manageable pieces makes it easier, we’ll tackle this problem in two parts.
First, we will show that the line segments are equal, and then we will show they are perpendicular.
Proving that line segments are equal
There are two hints in the problem statement that will guide us in formulating the strategy. One is that M is the midpoint of BC, and the other is that O and Q are the centers of squares.
Because M is given as a midpoint, we are guided to think of ways of using the triangle midpoint theorem where M is the midpoint of a side of a triangle. So we need to find triangles in which BC is a side.
Which triangles to use? This is where the second hint comes in - O and Q are the centers of squares, and a square is a regular polygon. So the distance from O and Q to the squares' vertices is the radius of this regular polygon. This means that they are both the midpoints of their squares' diagonals. Let's draw those:
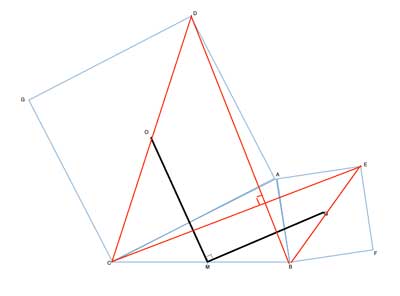
Now we have two triangles - ΔBCD and ΔBCE. In those triangles, OM and QM are the midsegments in each, since they connect the midpoints of two sides.
Using the triangle midpoint theorem, OM=½BD and QM=½CE. But as we have shown in another problem, when such squares are constructed on the sides of a triangle, BD=CE. So OM=QM.
Proving that line segments are perpendicular
Having shown that OM and QM are midsegments, we now make use of another property of midsegments: The midsegment is parallel to the third side.
So OM||BD and QM||CE. Referring again to the problems where we have dealt with such squares, we've shown that BD⊥CE. So, using the perpendicular transversal theorem once, OM⊥CE (OM||BD and BD⊥CE, so OM⊥CE). And using it again, OM⊥MQ (MQ||CE and OM⊥CE, so OM⊥MQ).
Proof
(1) CM=MB //Given
(2) CO=OD //O is the center of ACGD, so is the middle of diagonal CD
(3) BQ=QE //Q is the center of ABFE, so is the middle of diagonal BE
(4) OM=½BD //(1),(2),Triangle midsegemt theorem
(5) QM=½CE //(1),(3), Triangle midsegemt theorem
(6) BD=CD //Squares on the sides of triangles- proven in this lesson
(7) OM=QM //(4),(5),(6), Transitive property of equality
Now for the second part...
(8) OM||BD //(1),(2),Triangle midsegemt theorem
(9) QM||CE //(1),(3), Triangle midsegemt theorem
(10) BD⊥CE. //Squares on the sides of triangles- proven in this lesson
(11) OM⊥CE //(8), (10), perpendicular transversal theorem
(12)OM⊥MQ //(9), (11), perpendicular transversal theorem
