Squares On the Sides of a Triangle

The Pythagorean Theorem shows us an important property of the squares constructed on the sides of a right triangle, namely that c^{2 =} a²+b²:

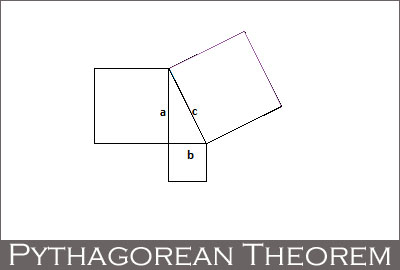
But there are interesting properties of squares constructed on the sides of any triangle, as we will explore in this geometry problem.

Problem

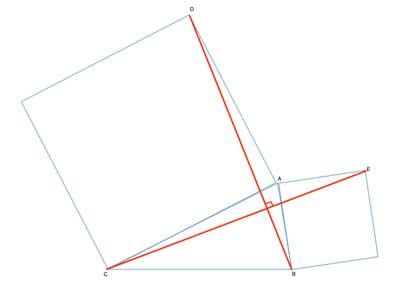
Two squares are constructed on sides AB and AC of triangle ΔABC. Show that CE=BD, and that CE⊥BD.

Strategy

We'll tackle this problem in two parts - first show that the line segments are equal, then show they are perpendicular.

Splitting complex problems into smaller, manageable pieces often makes it easier to see how to prove each part, separately.

Proving that line segments are equal

For the first part, we need to show that CE=BD, and as we commonly do, we will look to see if there are congruent triangles in which they are corresponding sides.

Let's look at the two triangles already provided in the problem statement, in which CE and BD are sides, triangles ΔACE and ΔADB.

We constructed squares on the sides of triangle ΔABC, and in a square all the sides are equal. So we already have two sides that are congruent: AD=AC and AB=AE. The thirds side is what we need to prove is equal (CE=BD), so obviously we can't rely on that.

Let's look for angles. Since we already have two congruent sides, the easiest way would be to use the Side-Angle-Side postulate, so let's look at the angles between the two congruent sides: ∠DAB and ∠CAE.

∠DAB is made up of ∠CAB plus a 90° angle (∠DAC)  from the square. Similarly, ∠CAE is made up of ∠CAB plus a 90° angle (∠BAE)  from the other square. So both of them are equal to m∠CAB + 90 and they are congruent. So the triangles are congruent, and CE=BD as corresponding sides.

Proving that line segments are perpendicular

Now let's turn to the second part, showing that the lines are perpendicular. To do this will need to show that one of the angles at the intersection point, X, is equal to 90°.

Let's see if we can get there using some angle math. We will make use of the fact that we have squares here where the angles are right angles.

Let's label ∠ACE 'γ'. We have proven that triangles ΔACE and ΔADB are congruent, so m∠ACE= m∠ADB=γ. Now, look at ∠AZD. It is an exterior angle to ΔDAZ, so by the exterior angle theorem, it is equal to the sum of the two remote interior angles - so it is equal to γ+90°.

But ∠AZD is also an exterior angle to ΔZCX, so by the exterior angle theorem, it is equal to the sum of the two remote interior angles - so it is equal to γ+m∠ZXC.

But if m∠AZD = γ+90° and m∠AZD = γ+m∠ZXC, then m∠ZXC=90° and CE⊥BD.

Proof

(1) AD=AC //Definition of a square
(2) AB=AE //Definition of a square
(3) m∠DAC=90° //Definition of a square
(4) m∠BAE=90° //Definition of a square
(5) ∠DAB ≅ ∠CAB +∠DAC //Angle addition postulate
(6) ∠CAE ≅ ∠CAB +∠BAE //Angle addition postulate
(7) ∠DAB ≅ ∠CAE //(3),(4),(5),(6), transitive property of equality
(8) ΔACE ≅ ΔADB //(1), (2), (7), Side-Angle-Side
(9) CE=DB //(8), Corresponding sides in congruent triangles (CPCTC)

Now let's formally prove the second part:
(10) ∠ACE≅∠ADB //(8), Corresponding side in congruent triangles (CPCTC)
(11) m∠ACE= m∠ADB=γ //Definition of congruent angles
(12) m∠AZD= γ+90° //Exterior angle theorem in ΔDAZ
(13) m∠AZD= γ+m∠ZXC //Exterior angle theorem in ΔZCX
(14) m∠ZXC=90° //(12), (13) , transitive property of equality
(15) CE⊥BD //(14), definition of perpendicular lines

We will use these two facts (CE=BD and CE⊥BD) in a subsequent problem.