Ratio of Areas of Triangles With the Same Height

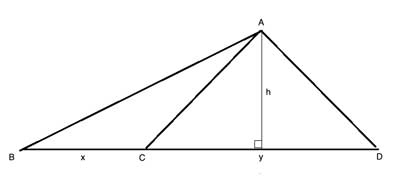
As the area of a triangle is given by the formula (base · height)/2, triangles with the same height will have areas whose ratio is the same as the ratio of their bases:

In the following geometry problem, we'll build on the proof we did to show that the diagonals of a parallelogram divide it into four triangles with equal areas, and apply this property to compare the lengths of two line segments.

Problem

ABCD is a parallelogram with diagonals AC and BD which intersect at point O. F is the midpoint of side BC (BF=FC). Find the ratio of AE to EF.

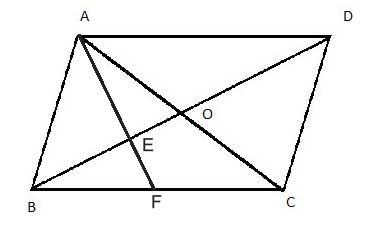
Strategy

When asked to compare ratios of line segments, we have two tools at our disposal- either similar triangles or triangles with same height or base.

Here we have intersecting diagonals of a parallelogram which we know create 4 triangles with equal areas. This is a hint to use the second of these methods.

Let's connect the vertex C with E, and look at the triangles ΔAOE and ΔCOE. In a parallelogram, the diagonals bisect each other so AO=OC. Both triangles have the same height, EG, so their areas must be equal. Let's call that area x.

Now, since BF=FC, the triangles ΔBEF and ΔCEF also have the same area (equal bases, and the same height, EH). We'll call that area y.

But, as we have already shown, the diagonals of a parallelogram divide it into four triangles with equal areas, so the area of ΔAOB is equal to the area of ΔCOB. The area of ΔCOB is (x+2y), and the area of ΔAOB is (x+ the area of ΔAEB), so the area of ΔAEB must be 2y.

Now, let's look at the triangles ΔAEB and ΔFEB. They share a vertex (B) and the base AF, so they both have the same height. And as stated in the beginning, triangles with the same height will have areas whose ratio is the same as the ratio of their bases.

So if the area of ΔAEB is 2y and the area of ΔFEB is y , the ratio of AE/EF must be 2:1.

Solution

(1) AO=OC //Diagonals of a parallelogram bisect each other
(2) EG=EG //Common height, reflexive property of equality
(3) Area_ΔAOE = Area_ΔCOE=x //(1), (2), triangles with equal bases and heights
(4) BF=FC //Given
(5) EH=EH //Common height, reflexive property of equality
(6) Area_ΔBEF = Area_ΔCEF=y //(1), (2), triangles with equal bases and heights
(7) Area_ΔAOB = Area_ΔCOB=(x+2y) // Diagonals of a parallelogram divide it into four triangles with equal areas
(8) Area_ΔAOB = Area_ΔAEB+x
(9) Area_ΔAEB=2y //(7), (8)
(10) Area_ΔAEB/ Area_AFEB=2 //(6), (9)
(11) AE/EF = 2 //Triangles with the same height have areas whose ratio is the same as the ratio of their bases