In another problem, we found the area of a parallelogram whose diagonals were perpendicular using the lengths of those diagonals and the lengths of one of its sides.
We actually only needed the length of the side in order to show that the diagonals were perpendicular. Once we established that, we knew this was a special parallelogram - one which is also a rhombus.
That made it easy to find the area, without even using the side, since the areas of a rhombus is just the product of its diagonals divided by two.
But as we mentioned in that problem, if we have the lengths of the diagonals and one side, we can compute the area for any parallelogram, even if the diagonals are not perpendicular. In this problem, we will show how to do this.
Problem
ABDC is a parallelogram with a side of length 11 units, and its diagonal lengths are 24 units and 20 units. Find its area.
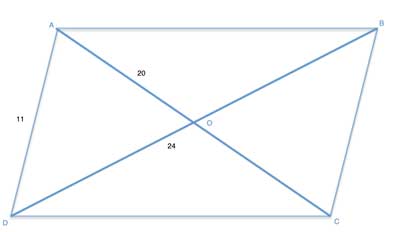
Strategy
The diagonals divide the parallelogram into 4 triangles. In another problem, we've seen that these 4 triangles have equal areas.
Even if we don't remember that, it is easy to reconstruct the proof we did there. We know the diagonals of a parallelogram bisect each other, so triangles ΔABO and ΔADO, for example, have the same size base and the same height - so they have an equal area.
And the same goes for any other pair of adjacent triangles in the parallelogram. So if we find the area of just one of these triangles, we'll have the area of the parallelogram by multiplying it by four.
Since the diagonals bisect each other and we know their lengths, we have the entire perimeter of triangle ΔADO. How to find the area of a triangle if we know its perimeter? We can use Heron's formula.
For a triangle with sides a, b, and c, the semi perimeter s is (a+b+c)/2. Heron's formula gives its area as √[s⋅(s-a)⋅(s-b)⋅(s-c)].
We can now plug in our problem's values for a, b and c, get the area of triangle ΔADO, and then multiply by 4 to get the area of the parallelogram.
Solution
(1) a= 11 //given
(2) b=10 //AC=20, given, the diagonals of a parallelogram bisect each other so AO=10
(3) c=12 //BD=24, given, the diagonals of a parallelogram bisect each other so DO=12
(4) s=(a+b+c)/2=(11+10+12)/2=16.5 //(1), (2),(3), substitution
(5)AΔADO=√[s⋅(s-a)⋅(s-b)⋅(s-c)] //Heron's Formula
(6) AΔADO=√[16.5*(16.5-10)*(16.5-11)*(16.5-12)]=√2654.4375≈51.52
(7)AABCD=4*AΔADO //The diagonals divide the parallelogram into 4 triangles of equal areas
(8) AABCD= 206.08
Note
It is worth mentioning that you can't get the area of the parallelogram using only the diagonals. In addition, you must have either the length of one side, or one of the angles of the parallelogram. To understand why, in a visual way, think of the diagonals as two rigid sticks, connected at their point of intersection by a loose screw or nail. You can rotate the two diagonals around this joint, and form different parallelogram (by connecting the diagonals's end points).
These parallelograms have different areas. If you make the diagonals almost parallel to one another - you will have a parallelogram with a height close to zero, and thus an area close to zero. But as you create a larger angle between the diagonals, the area of the parallelogram will increase.
