This post will be a short and simple but very useful application of the general formula for finding the area of a triangle, to the specific case of a right triangle.
Problem
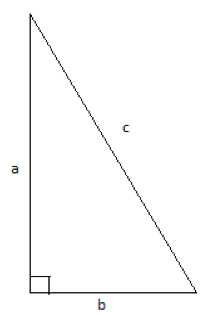
ΔABC is a right triangle with legs a and b, and hypotenuse c. Find a formula for its area using these sides.
Strategy
The general formula for the area of a triangle is the base times the height to that base, divided by two.
This usually requires us to draw a line, called height or altitude, from one vertex of the triangle to the side opposite it, which is perpendicular to that side.
But in a right triangle, these lines already exist- they are the legs of the triangle. By definition, a right triangle has a 90° angle between its legs, so they are perpendicular to each other.
The height to leg a is b, and vice verse, the height to leg b is side a. So the area of a right triangle is simply the product of the two legs, divided by two: a·b/2
Let's see a simple application of this - finding the area of a rhombus, given the lengths of its diagonals. We know that in a rhombus, the diagonals are perpendicular to each other, partitioning the rhombus into 4 right triangles.
We also know that the diagonals bisect each other. So each of these 4 triangles has an area of [(half of one diagonal) x (half the other diagonal)]/2, or diagonal1 x diagonal2/8.
But we have four of these in the rhombus, so the area of the rhombus is, as we have seen elsewhere, the half product of its diagonals.
As you can see, this was a simple but useful application of the formula for finding the area of a right triangle.