A rhombus is a special kind of parallelogram, in which all the sides are equal. We've seen that one of the properties of a rhombus is that its diagonals are perpendicular to each other. Here we will show the converse- that if a parallelogram has perpendicular diagonals, it is a rhombus - all its sides are equal.
Problem
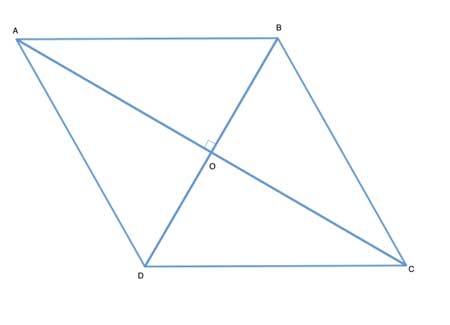
ABCD is a parallelogram, and its diagonals are perpendicular - AC⊥DB. Show that ABCD is a rhombus.
Strategy
ABCD is a rhombus if all its sides are equal. We know that the opposite sides in ABCD are equal, because it is a parallelogram. So we need to show that one pair of adjacent sides is equal. We will do this using congruent triangles.
Let's take triangles ΔAOD and ΔCOD. We have one common side - OD, and since the diagonals are perpendicular, m∠AOD = m∠COD=90°, and so ∠AOD ≅ ∠COD. We now need either another side, or another angle to show the triangles are congruent.
So let's review the properties of parallelograms - one of them is that the diagonals bisect each other. So |AO|=|OC|, and we have our second side for the Side-Angle-Side postulate.
And if triangles ΔAOD and ΔCOD are congruent, |AD|=|DC|, and we are done showing that a parallelogram with perpendicular diagonals is a rhombus.
Proof
(1) |AD|=|BC| ; |AB|=|DC| //Opposite sides of a parallelogram are equal
(2) |OD|=|OD| //Common side, reflexive property of equality
(3) AC⊥DB //Given
(4) m∠AOD = m∠COD=90° // (3), definition of perpendicular lines
(5) ∠AOD ≅ ∠COD // (4), definition of congruent angles
(6) |AO|=|OC| // diagonals of a parallelogram bisect each other
(7) ΔAOD≅ΔCO // (2), (5), (6). Side-Angle-Side postulate
(8) |AD|=|DC| // Corresponding sides in congruent triangles (CPCTC)
(9) |AD|=|BC|=|DC|=|AB| // (1),(8)
(10) ABCD is a rhombus //(9), defintion of a rhombus (parallelogram with equal sides)
