Today we will prove Heron's formula for finding the area of a triangle when all three of its sides are known. The proof is a bit on the long side, but it's very useful.
In another post, we saw how to calculate the area of a triangle whose sides were all given, using the fact that those 3 given sides made up a Pythagorean Triple, and thus the triangle is a right triangle. But what if we have 3 sides of a triangle which is not a right triangle?
It turns out we can still figure out its area, without proving any additional theorems or using trigonometry. We'll just use what we already know about the area of triangles and the Pythagorean Theorem.
But there will be a lot of calculations involved- algebra and substitutions, so patience is required - this is known as Heron's formula.
Problem
Triangle ΔABC has side lengths a, b, and c. Find a formula for its area using the 3 sides.
Strategy
What do we know about the area of a triangle? It is the base times the height to that base, divided by two. Here, we have all three sides, so we could use any of them as a base. But we have no height to any of them - so let's draw such a height, to side AB:
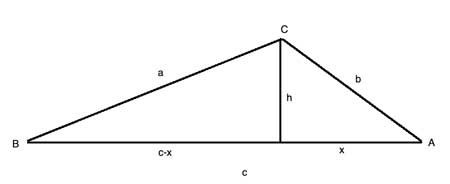
So now we have two right triangles, with the same height, h. Using the Pythagorean Theorem we can derive an expression for both x and h, using just a, b, and c.
Solving for x
From the right triangle on the right side, we have
h2+x2 = b2, or h=√(b2-x2)
But also from the right triangle on the left side:
h2+(c-x)2 = a2, or h=√(a2-(c-x)2) = √(a2-c2+2cx-x2)
So √(b2-x2) =√(a2-c2+2cx-x2), and since all the lengths here are positive quantities, we can just eliminate the radical, and get b2-x2=a2-c2+2cx-x2. Simplifying and rearranging we have:
a2-b2=c2+2cx, and we can now solve for x:
x= (-a2+b2+c2)/2c
Now we can substitute that back into one of the equalities we had above: h2+x2 = b2, so h2= b2-x2 and plugging the formula for x into that we get h2=b2-[(-a2+b2+c2)/2c]2
From our knowledge of algebra, we have an identity for the differences of squares:
x2-y2 =(x+y)((x-y). Using b for x and [(-a2+b2+c2)/2c] for y we get
h2=(b+[(-a2+b2+c2)/2c)(b-[(-a2+b2+c2)/2c)=(2bc-a2+b2+c2)(2bc+a2-b2-c2)/4c2.
Now let's simplify and rearrange this a bit, by repeatedly applying the identity for the differences of squares:
h2=(2bc-a2+b2+c2)(2bc+a2-b2-c2)/4c2= [(b+c)2-a2][a2-(b-c)2]/4c2=[(b+c)+a][(b+c)-a][a+(b-c)][a-(b-c)]/4c2
And from this, h= √([b+c+a][(b+c-a][a+b-c][a+c-b])/2c
Ok, now we are basically done - we have defined h in terms of a,b, and c, and since the area of the triangle is h⋅c/2, we could simply multiply and get
(*) AABC=¼⋅√([b+c+a][(b+c-a][a+b-c][a+c-b])
Simplifying the formula further
As I said, this formula is complex. So let's play around with the lengths a little bit, to get an even simpler formula, and an interesting result.
Since a, b, and c are the sides of the triangle, a+b+c is its perimeter. Let's define s as half the perimeter, or semiperimeter: s= (a+b+c)/2.
From this defintion, (b+c+a) = 2s; (b+c-a)=2(s-a); (a+b-c) = 2(s-c) and (a+c-b)=2(s-b). Plugging these into (*) above we get:
AABC=¼⋅√([b+c+a][(b+c-a][a+b-c][a+c-b])=¼⋅√[2s⋅2(s-a)⋅2(s-b)⋅2(s-c)]=
=¼⋅√[16s⋅(s-a)⋅(s-b)⋅(s-c)]=√[s⋅(s-a)⋅(s-b)⋅(s-c)]
