There are several ways to find the area of a rhombus. A rhombus is a special kind of parallelogram, in which all the sides are equal.
Because it is a parallelogram, we can find its area using the general formula for the area of a parallelogram - the length of a side times the hight to that side.

But a rhombus is also a kind of a kite - a kite in which all the sides are equal. So we can also use the formula for an area of a kite to get the area of a rhombus.
We've seen that if we know the lengths of a kite's diagonals, the area of the kite is the product of the lengths of these diagonals, divided by two.
Let's derive this formula for a rhombus, directly.
Problem
ABCD is a rhombus. Find a formula for its area using the lengths of its diagonals |AC| and |BD|.
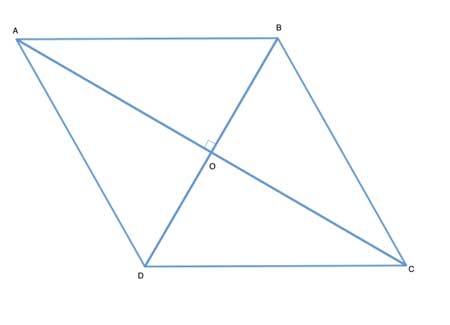
Strategy
We'll start out the same way as we did when we derived the formula for the area of a kite, by using the technique of partitioning the kite into simpler shapes. The diagonals have already partitioned the rhombus into four triangles, ΔADO, ΔABO, ΔCBO and ΔCDO.
We know the diagonals of a rhombus are perpendicular to each other, and they bisect each other. And we've also seen that the diagonals of a parallelogram divide it into 4 equal areas.
So all we have to do is find the area of one of these triangles (ΔADO, ΔABO, ΔCBO or ΔCDO), and multiply by 4 to get the area of the rhombus.
Let's take triangle ΔADO. The diagonals of the rhombus are perpendicular, so it is a right triangle, whose area is (leg x leg) / 2. And because the diagonals bisect each other, its two legs' lengths are equal to half of each diagonal. So its area is |AC|/2 times |BD|/2, divided by two.
The area of the rhombus is 4 times this, so it is 4 • (|AC|/2 • |BD|/2)/2., or after simplifying, |AC|• |BD|/2
Solution
(1) |AO|=|AC|/2 //diagonals of a parallelogram bisect each other
(2) |DO|=|DB|/2 //diagonals of a parallelogram bisect each other
(3) AreaAOD=|AO|•|DO|/2 // Area of a triangle
(4) AreaAOD=(|AC|/2 • |DB|/2)/2 //(1), (2), (3)
(5) AreaABCD = 4 • AreaAOD //Diagonals of a parallelogram divide it into 4 equal areas.
(6) AreaABCD = 4 • (|AC|/2 • |DB|/2)/2 //(4), (5)
(7) AreaABCD=|AC|• |DB|/2
