In this problem we will prove the Reverse Triangle Inequality Theorem, using what we have already proven In a previous problem- the Triangle Inequality.
The Triangle Inequality theorem states that in a triangle, the sum of the lengths of any two sides is larger than the length of the third side.
The Reverse Triangle Inequality states that in a triangle, the difference between the lengths of any two sides is smaller than the third side. Or stated differently, any side of a triangle is larger than the difference between the two other sides.
In addition to formally proving that theorem, we also provided an intuitive explanation of why it is true, using what we know about the shortest distance between two points - it is the straight line connecting them.
We can think of any triangle as being composed of one side, which is the straight line between two points. The other two side are another path between those two points. But that path goes through a third point. Since this is not the straight line, going through that path it is going to be longer. So the sum of the two sides which form the alternate path is longer than the straight line.
Here, we will do the same - we will provide a formal proof of the theorem, and then give an intuitive explanation of why it is true.
Problem
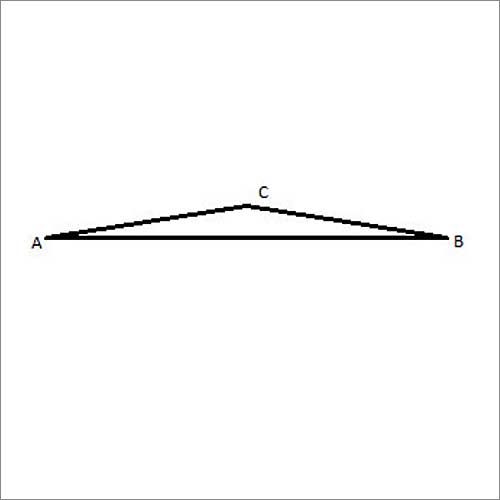
Show that |AB|>||AC|-|CB||, |AC|>||AB|-|CB|| and |BC|>||AB|-|AC||
Strategy
We will use the Triangle Inequality Theorem we have already proven, and do a little manipulation of the lengths, using basic algebra to get the desired result.
Proof
(1) |AB| + |AC| > |CB| //Triangle Inequality Theorem
(2) |AB| + |AC| -|AC| > |CB|-|AC| //(1) Subtracting the same quantity from both side maintains the inequality
(3) |AB| > |CB| - |AC| = ||AC|-|CB|| //(2), properties of absolute value
And similarly for the other two sides:
(4) |AB| + |AC| - |AB| > |CB|-|AB| // (1) Subtracting the same quantity from both side maintains the inequality
(5) |AC| > |CB|-|AB| = ||AB|-|CB|| //(4), properties of absolute value
(6) |AC|+|BC| > |AB| //Triangle Inequality Theorem
(7) |AC| + |BC| -|AC| > |AB|-|AC| //(6) Subtracting the same quantity from both side maintains the inequality
(8) |BC| > |AB| - |AC| = ||AB|-|AC|| //(7), properties of absolute value
Intuitive explanation
So, now that we have formally proven the Reverse Triangle Inequality, let's try to intuitively explain why this is so:
Imagine that you walk from point A to point B, and that is one side of a triangle. Then you walk from point B to C, in any direction. BC is the second side of the triangle. Because the shortest distance between two points is a straight line, the closest you could be to point A is if you traced your steps directly back toward A, on the same line, to point D.
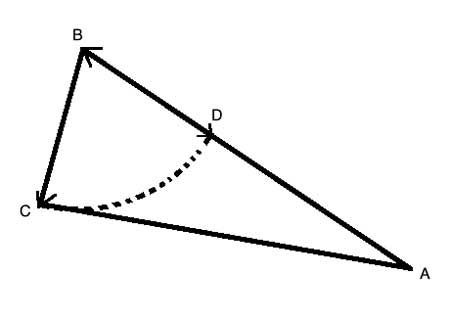
BD is the same length as BC, so AD is the difference between the two sides AB And BC. It is also smaller than AC, because D is the closest you could be to A after walking from B. But AC is the third side of the triangle, and is larger than AD, which is the difference between the two sides.
