In today's lesson, we combine several theorems (triangle midsegment theorem; Pythagorean Triples) to solve a difficult problem dealing with midpoints of a quadrilateral.
Sometimes, we are presented with problems that rely on utilizing more than one basic concept. When the two concepts are unrelated, it's difficult to connect the two in order to solve the problem. Here is one such example.
Problem
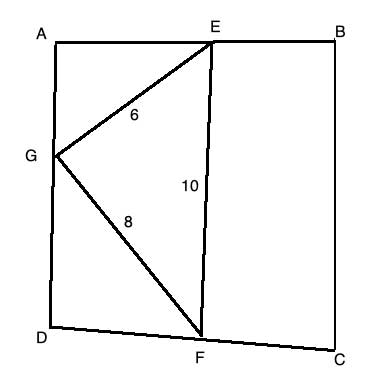
In quadrilateral ABCD, E, F and G are the midpoints of segments AB, CD and DA , respectively. Find the area of the quadrilateral.
Strategy
Let's try to piece out the hints given in the problem statement as to which concepts we need to apply here.
We have midpoints of segments, which should remind us of the Triangle Midsegment Theorem. The midsegment is parallel to the third side, and its length is equal to half the length of the third side. So we probably need to construct triangles in which these segments are sides.
We also need to find the area of the quadrilateral, but we can't use any of the standard formulas, because it is not a special quadrangle like a parallelogram or a rectangle.
The technique we use in such case is to partition the quadrilateral into simpler shapes where we can use known formulas (like we did for a trapezoid). This again points us in the direction of creating two triangles by drawing the diagonals AC and BD:

The area of the quadrilateral is the combined area of the two triangles, ΔADC and ΔABC.
The diagonals also created two triangles, ΔADC and ΔADB in which FG and GE are midsegments. So from the Triangle Midsegment Theorem, applied to ΔADC, we get that FG = ½AC, and since it is given that FG=8, AC=16.
And applying the Triangle Midsegment Theorem to the triangle ΔADB, we get that GE = ½DB, and since it is given that FG=6, AC=12.
AC is the base of both triangles, so if we find their height, we can calculate their area and get the area of the quadrilateral. But how do we find their height?
Finding the height of the triangles
Let's look at the final thing given in the problem definition, which we haven't used yet - the length of segment EF. The three sides of the triangle ΔEGF are 6, 8, and 10. Which should immediately jump out at us as a Pythagorean Triple - meaning that ΔEGF is a right triangle, and m∠EGF=90°.
Form the Triangle Midsegment Theorem, GF||AC and GE||DB, so if m∠EGF=90°, m∠GYZ=90° as it is the supplementary angle of two parallel lines (GE and DB), and also m∠YZX=90°, again as it is the supplementary angle of two parallel lines (GF and AC).
If m∠YZX=90°, that means that DB is perpendicular to AC, a d the segments DZ and BZ are the heights of the two triangles, ΔADC and ΔABC.
Let's call the length of segment DZ "h". Then segment BZ is DB-h.
The area of ΔADC is ½·h·AC, and the area of ΔABC is ½·(DB-h)·AC. The area of the quadrilateral is the combined area of the two triangles, so it is ½·h·AC+½·(DB-h)·AC, or ½·[h+(DB-h)]·AC.
Simplifying, we get ½·DB·AC, and as we already found the lengths of DB and AC (12 and 16, respectively), the area of the quadrilateral is ½·12·16, or 96.
This was a difficult one!
Don't be too concerned if this problem stumped you, initially. It is quite complex. In fact, variations of it have appeared in a number of national math competitions.
Alternatively, if you enjoyed the challenge of this complex problem, take a look at another similarly challenging one.
