If joining the midpoint of a rhombus forms a rectangle, what is the shape of the quadrilateral formed by joining midpoints of a rectangle? If you guessed it is a rhombus, you are correct, as we will now show.
Problem
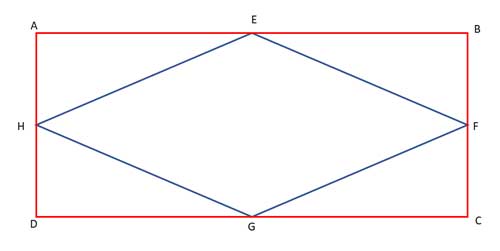
Strategy
As we have done before, in order to save us some work, we will rely on what we have already proven. A rectangle is a quadrilateral, so connecting its midpoints creates a parallelogram. To prove this parallelogram Is a rectangle, we need to show that all of its sides are equal.
Since this quadrilateral is a parallelogram, we already know that the opposite sides are equal, as this is a property of parallelograms. All that remains to be shown, then, is that two adjacent sides of the parallelogram are equal.
Sides EH and GH are two such adjacent sides, and they are also the sides of tow triangles, ΔEHA and ΔGHD. So let’s try to show those two triangles are congruent, proving that |EH|=|GH| as corresponding sides in congruent triangles.
To do so, we will rely on the fact that ABCD is a rectangle, and use the properties of rectangles: the opposite sides are equal (since a rectangle is a parallelogram), and the interior angles of a rectangle are all right angles (by definition).
And if the opposite sides are equal, then so are their halves. Since E and G are both midpoints, |AE|=|DG|, as halves of equal sides. H is also a midpoint, so |AH|=|HD|.
The angles of the rectangle are all equal and all measure 90°, so ∠EAH ≅ ∠GDH. We have now shown that ΔEHA and ΔGHD are congruent by the Side-Angle-Side postulate, and as a result |EH|=|GH| as corresponding sides in congruent triangles. And since |EH|=|FG| and |EF|=|HG|, it follows that all the edges are equal and EFGH is a rhombus.
Proof: the quadrilateral formed by joining midpoints of a rectangle is a rhombus
(1) ABCD is a rectangle //Given
(2) |AE|=|EB| //Given
(3) |BF|=|FC| //Given
(4) |CG|=|GD| //Given
(5) |DH|=|HA| //Given
(6) |AB|=|DC| //(1), Opposite sides of a rectangle are equal
(7) ½|AB|=½|DC| //Division Property of Equality
(8) |AE|=|DG| //(6), (7)
(9) ∠EAH ≅ ∠GDH //All interior angles of a rectangle are equal
(10) ΔEHA ≅ ΔGHD //(5), (8), (9) , Side-Angle-Side postulate
(11) |EH|=|GH| //Corresponding sides in congruent triangles (CPCTC)
(12) EFGH is a parallelogram //connecting midpoints of a quadrilateral creates a parallelogram.
(13) |EH|=|FG| ; |EF|=|HG| //(12) Opposite sides of a parallelogrm are equal
(14) |EH|=|GH| =|FG|=|FE| //(13), (11)
(15) EFGH is a rhombus //(14), definition of a rhombus
