Finding the Length of a Common Chord

If we know the radii of two intersecting circles, and how far apart their centers are, we can calculate the length of the common chord.

Problem

Circles O and Q intersect at points A and B. The radius of circle O is 16, and the radius of circle Q is 9. Line OQ connects the centers of the two circles and is 20 units long. Find the length of the common chord AB.

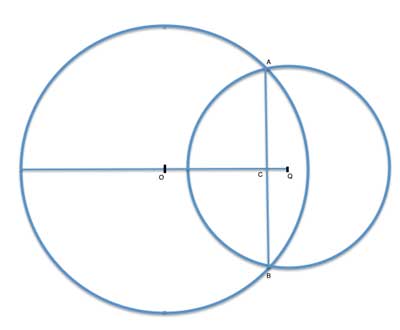
Strategy

We know that line OQ is the perpendicular bisector of the common chord AB. And we are also given the lengths of the radii, so we probably need to use that. Let's draw these radii:

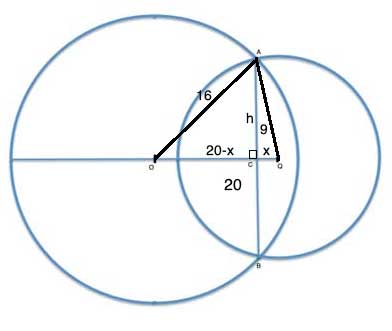
Now, we have two triangles, △AOC and △AQC. They are both right triangles (since OQ is perpendicular to AB), and both have the same height, h. If the base of one of these is x units long, the other base is 20-x, as OQ is 20 units long.

Now, using the Pythagorean Theorem and some basic algebra, we can solve the following system of equations for x:

(1) h²+(20-x)²=16² (in right triangle △AOC)
(2) h²+x²=9² (in right triangle △AQC)

And once we find x, we substitute it in one of the above equations to find h. AB is 2h, since OQ is a bisector of AB.

Solution

(1) AB⊥OQ //Line connecting centers is perpendicular to common chord
(2) △AOC, △AQC are right triangles
(3) h²+(20-x)²=16² //(2), Pythagorean theorem
(4) h²+x²=9² //(2), Pythagorean theorem
(5) 400-40x = 256-81 //Subtract (4) from (3)
(6) x=225/40=5.625
(7) h²=81-31.64
(8) h=√49.36=7.03
(9) AB=14.06