We have already shown that the diagonal that connects the two corners formed by the sides that are equal bisects the angles at those corners. So it is now easy to show another property of the diagonals of kites- they are perpendicular to each other.
Problem
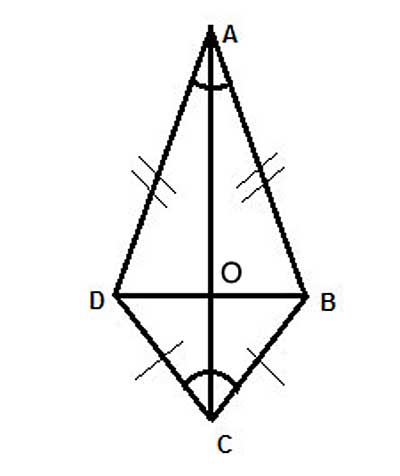
ABCD is a kite. Show that the diagonals are perpendicular, that is, AC⊥DB.
Strategy
We will follow the exact same strategy as we did to prove a very similar theorem - that the Diagonals of a rhombus are perpendicular to each other. And we will use triangle congruency.
In addition, we will also use what we've earlier proved for kites- that the diagonal that connects the two corners formed by the sides that are equal bisects the angles at those corners.
Using the above, we can show that triangles ΔAOD and ΔAOB are congruent using the Side-Angle-Side postulate, and from that, that ∠AOD ≅ ∠AOB.
And now, since ∠AOD and ∠AOB are a linear pair, we use the Linear Pair Perpendicular Theorem – If two straight lines intersect at a point and form a linear pair of equal angles, they are perpendicular.
Proof
(1) ABCD is a Kite //Given
(2) AB=AD //(1) definition of a kite
(3) AO=AO //Common side, reflexive property of equality
(4) ∠BAC ≅ ∠DAC // (1), in a kite the axis of symmetry bisects the angles at those corners
(5) △AOD≅△AOB //Side-Angle-Side postulate.
(6) ∠AOD ≅ ∠AOB //Corresponding angles in congruent triangles (CPCTC)
(7) AC⊥DB //Linear Pair Perpendicular Theorem
Using this property, it is easy to find a formula for the area of a kite, using the lengths of its diagonals.
