In today's lesson, we will prove that the diagonal of a kite which forms the axis of symmetry (connecting the two corners formed by the equal sides) bisects the other diagonal.
As you probably know, a deltoid has two diagonals. One connects the two corners formed by the sides that are equal. And the other diagonal connects the two corners formed by the two unequal sides.
The diagonal that connects the two corners formed by the sides that are equal forms the (one and only) axis of symmetry of the deltoid.
We have already shown that when we “fold” the deltoid over this line of symmetry the two parts will match – and thus this diagonal bisects the angles at its endpoints.
Using the same approach, we will now show that since the folded parts match, the axis of symmetry also bisects the other diagonal.
Problem
In a deltoid ABCD, show that the diagonal forming the axis of symmetry bisects the other diagonal, DO=OB.
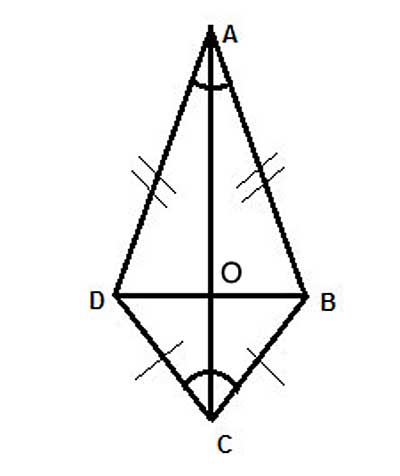
Strategy
The axis of symmetry is the diagonal AC. We used the Side-Side-Side postulate to show that it bisects the angles at its endpoints.
We can now use this fact to show that the smaller triangles formed by the diagonal AC and the other diagonal are also congruent.
By using the Side-Angle-Side postulate, we prove that the corresponding sides, OD and OB, are congruent. Thus, the diagonal AC bisects the diagonal DB. And we have our proof!
Proof
(1) ABCD is a Kite //Given
(2) AB=AD //(1) definition of a kite
(3) AO=AO //Common side, reflexive property of equality
(4) ∠BAC ≅ ∠DAC // (1), in a kite the axis of symmetry bisects the angles at those corners
(5) △AOD≅△AOB //Side-Angle-Side postulate.
(6) OD ≅ OB //Corresponding sides in congruent triangles (CPCTC)
