An obtuse triangle is a triangle in which one of the angles is larger than 90°. There is only one such angle possible, since the sum of angles in a triangle is 180°.
It's easy to show that in this type of triangle, the obtuse angle is larger than the sum of the other two angles.
It's also easy to show the converse- that if an angle in a triangle is larger than the sum of the other two, then the triangle is obtuse. Both of these follow directly from the fact that the sum of angles in a triangle is 180°.
Problem
Show that in an obtuse triangle, the obtuse angle is larger than the sum of the other two angles. Also show the converse- that if an angle in a triangle is larger than the sum of the other two, then the triangle is obtuse.
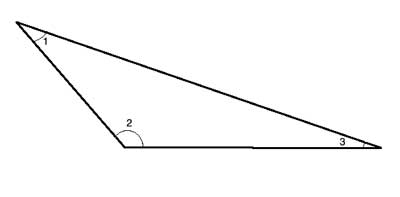
Strategy
Both of these problems are a direct consequence of the fact that the sum of all three angles in a triangle is exactly 180°. So our strategy is to prove them using arithmetic manipulation of the sum of the angles.
Proof
(1) m∠1 + m∠2 + m∠3= 180° //sum of angles in a triangle is 180°
(2) m∠2>90° // Given, ΔABC is obtuse
(3) m∠1 + m∠3 < 90° // subtract (2) from (1)
(4) m∠1 + m∠3 < m∠2 //(2), (3)
Now lets do the converse, show that if m∠1 + m∠3 < m∠2, then ΔABC is obtuse:
(5) m∠1 + m∠2 + m∠3= 180° //sum of angles in a triangle is 180°
(6) m∠1 + m∠3 < m∠2 // Given
(7) m∠2 >180° -m∠2 // subtract (6) from (5)
(8) 2 * m∠2 > 180° //Add m∠2 to both sides
(9) m∠2 > 90° //divide by 2
(10) ΔABC is obtuse //(9) , defintion of obtuse triangle
