Using the technique of partitioning a complex shape into simpler geometric shapes, with known formulas for their areas, we can find a simple formula for the area of a kite. It is the product of the lengths of its diagonals, divided by two.
Problem
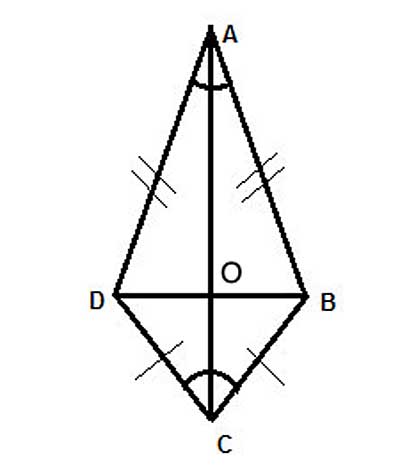
ABCD is a kite, with diagonal AC=x and diagonal BD=y. Find a simple formula for the area of the kite.
Strategy
As we said in the introduction, we'll use the technique of partitioning the kite into simpler shapes. The kite is composed of the two triangles ΔADB and ΔCDB. DB is the base of both these triangles, and its length is given (y).
We know the diagonals of a kite are perpendicular to each other. So OC is the height of triangle ΔCDB, and OA is the height of triangle ΔADB. Let's call the lengths of OC 'z', then since AC=x, the length of OA is x-z.
The area of a triangle is given by the formula Area = (h · b) /2, so the area of ΔCDB is z·y/2, and the area of ΔADB is (x-z)·y/2. The area of the kite is the sum of the areas of these triangles, or z·y/2+(x-z)·y/2.
Simplifying, z·y/2+(x-z)·y/2 =(z·y+x·y-z·y)/2=x·y/2, so the area of the kite is the product of the lengths of its diagonals, divided by two.
