Consecutive Interior Angles Theorem

The Theorem

The Consecutive Interior Angles Theorem states that the two interior angles formed by a transversal line intersecting two parallel lines are supplementary (i.e: they sum up to 180°).

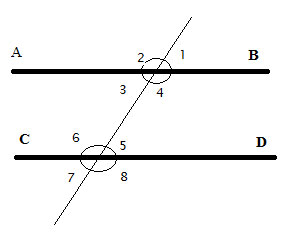
The problem

AB||CD, prove m∠5 + m∠4 = 180°, and that m∠3 + m∠6 = 180°

So how do we go about this? We already know that the two angles that are next to each other and which form a straight line are “Supplementary angles” and their sum is 180°. So we will try to use that here, too, since here we also need to prove that the sum of two angles is  180°.

So let’s proceed to the proof, using what we already know about angles that are next to each other and which form a straight line.

Proof

Here's how you prove the Consecutive Interior Angles Theorem:

(1)    AB||CD                                 //given
(2)    ∠1 ≅ ∠5                                //from the axiom of parallel lines – corresponding angles
(3)    m∠1 = m∠5                        //definition of congruent angles 
(4)    m∠1 + m∠4 = 180°           //straight line measures 180° 
(5)    m∠5 + m∠4 = 180°           //using (3) and (4), and performing algebraic substitution, replacing  m∠1 with the equivalent m∠5

And we can repeat this proof for the second pair of interior angles. We'll replace m∠1 with  m∠2, m∠5 with m∠6 and m∠4 with m∠3

And we have proven the theorem.