We've seen that when a square is inscribed in a circle, we can express all the properties of either the square or circle (area, perimeter, circumference, radius, side length) if we know just the length of the radius or the length of the square's side.
Now we'll see that the same is true when the circle is inscribed in the square.
Problem 1
A circle with radius ‘r’ is inscribed in a square. Find formulas for the square’s side length, diagonal length, perimeter and area, in terms of r.
Strategy
In solving the similar problem of a square is inscribed in a circle, the key insight was that the diagonal of the square is the diameter of the circle.
Here, a similar key insight is that the circle's radius is equal to half the square's side length.
Since the circle is inscribed in the square, the square's side is tangent to the circle. By definition, the radius is perpendicular to the tangent line at the point of tangency.
The radius forms a 90° angle with one side of the square. Thus, it is parallel to the adjacent side of the square. This is true for the other radii, as well. That means that the quadrilateral formed by two radii and two adjacent sides of the square is also a square.
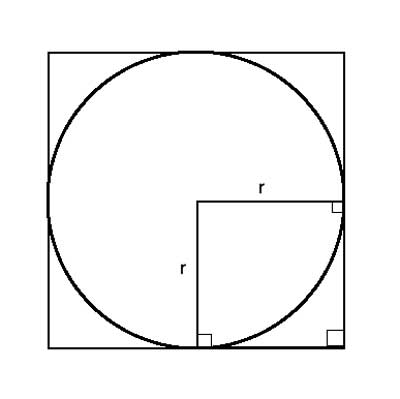
In this new small square, the side is equal to the radius. We can do this for each of the other 4 sides of the larger, outer square. In each one of them, the radii will form smaller squares. In the smaller squares, the sides are all equal to the radius.
The sides of two such adjacent small squares form the side of the larger outer square. Since each one of the smaller square's sides is equal to r, the side of the outer square is 2r.
Formal proof:
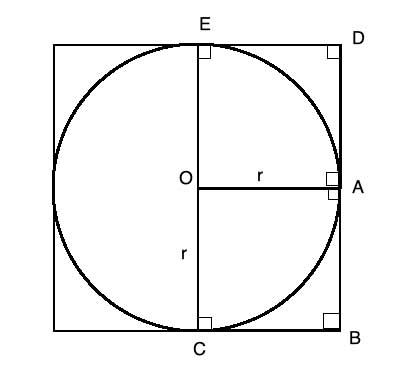
(1) OA ⊥ AB //Given, AB is tangent to circle O, a tangent line is perpendicular to the radius
(2) m∠OAB=90° //Definition of perpendicular line
(3) m∠ABC=90° //All interior angles of a square are right angles
(4) OA||CB //Converse Consecutive Interior Angles Theorem
(5) OC ⊥ CB //Given, CB is tangent to circle O, a tangent line is perpendicular to the radius
(6) m∠OCB=90° //Definition of perpendicular line
(7) m∠ABC=90° //All interior angles of a square are right angles
(8) OC||AB //Converse Consecutive Interior Angles Theorem
(9) OC=OA //All radii of a circle are equal
(10) OCBA is a parallelogram //(4), (8), definition of a parallelogram
(11) BA=OC=r //opposite sides of a parallelogram are equal
And similarly,
(12) OEDA is a parallelogram
(13) AD=OE=r //opposite sides of a parallelogram are equal
(14) |BD|=|BA|+|AD| = r + r = 2r
Ok, now that we have done that, the rest is very easy. The square's area is side length squared, so it is 4r2. The perimeter is 4 times the side length, so it is 8r. And the length of the diagonal can be calculated using the Pythagorean theorem, and it is 2r√2.
Now let’s do the converse, finding the inscribed circle’s properties from the length of the side of the square.
Problem 2
A circle is inscribed in a square, with a side measuring 'a'. Find formulas for the circle's radius, diameter, circumference and area , in terms of 'a'.
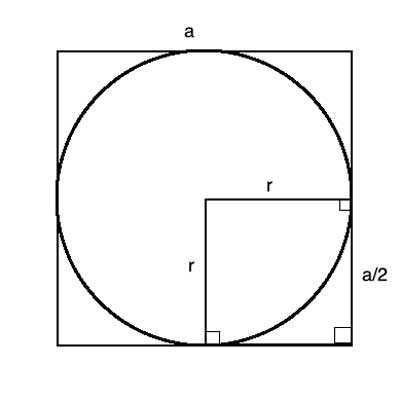
As we've shown above, the circle's radius is equal to the half the length of the square's side, so r=a/2. The diameter is twice the radius, so d=a. The circumference is d ·π, so C=πa. Finally, the area is π·r2, so A= π·a2/4.
These type of inscribed shape problems often have a component of finding the area between the shapes, which is irregular, so let's explore an example.
Problem 3
A circle is inscribed in a square, with a side measuring 10 units. Find the area of the shaded region:
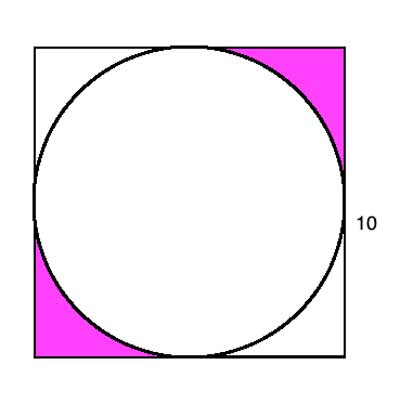
Strategy
The key to solving these type of problems is to find the areas of the regular shapes. Then, express the shaded area as the difference between them. In this case, we can easily find the area of the circle and the square.
The difference between them is the 4 corner shapes formed by two edges of the square and an arc which is a quarter of the circle. From symmetry, all these shapes have equal area. So the shaded region is half the difference between the areas of the circle and the square.
Solution
Asquare=a·a=10·10=100
Acircle= π·a2/4=π·102/4=25π
Ashaded=(Asquare-Acircle)/2=(100-25π)/2=12.5(4-π)