In today's lesson, we will prove the Converse of the Corresponding Angles Theorem. We will use the very useful technique of proof by contradiction.
We had earlier said axiomatically, with no proof, that if two lines are parallel, the corresponding angles created by a transversal line are congruent.
Now let’s prove an important converse theorem: that if 2 corresponding angles are congruent, then the lines are parallel.
Prove:
If 2 corresponding angles formed by a transversal line intersecting two other lines are congruent, then the two lines are parallel.
Strategy: Proof by contradiction
To prove this, we will introduce the technique of “proof by contradiction,” which will be very useful down the road.
When we use a “proof by contradiction” method, we start by assuming that what we are trying to prove is NOT true, and we proceed from there until we reach an impossible conclusion – a contradiction.
This means that our original assumption is false (as it leads to this impossible situation), and thus what we were trying to prove must be true.
Proof
So, let’s say we have two lines L1, and L2 intersected by a transversal line, L3, creating 2 corresponding angles, 1 & 2 which are congruent (∠1 ≅ ∠2, m∠1=∠2).
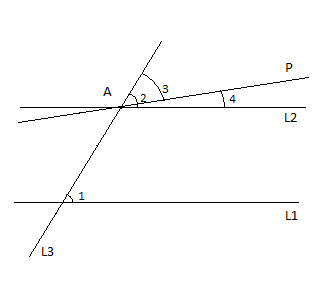
We want to prove the L1 and L2 are parallel, and we will do so by contradiction. Assume L1 is not parallel to L2. Then, according to the parallel line axiom we started with (“for every straight line and every point not on that line, there is one straight line that passes through that point which is parallel to the first line”), there is a different line than L2 that passes through the intersection point of L2 and L3 (point A in the drawing above), which IS parallel to L1.
Let’s draw that line, and call it P. Let’s also call the angle formed by the traversal line and this new line angle 3, and we see that if we add some other angle, call it angle 4, to it, it will be the same as angle 2.
Now, P||L1 so ∠1 ≅ ∠3, as corresponding angles formed by a transversal of parallel lines, and
This contradicts what was given, that angles 1 and 2 are congruent! This contradiction means our assumption (“L1 is not parallel to L2”) is false, and so L1 must be parallel to L2.