Shortest Distance Theorem

The Shortest Distance Theorem states that the shortest distance between a point P, and a line, l, is the perpendicular line from P to l.  It is also called the "perpendicular distance."

It is simple to prove this theorem using the Pythagorean Theorem.

Problem

Prove that the shortest distance between a point P, and a line, l, is the perpendicular line from P to l.

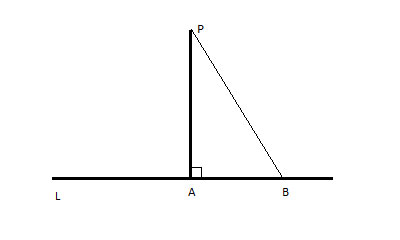
Strategy

Since the perpendicular line from P to l forms a right angle, we will try to use what we know about right triangles, and the theorem we have about lengths of the sides of a right triangle - the Pythagorean Theorem.

Any line from P to l other than the perpendicular line PA will form a right triangle, where that new line is the hypotenuse.

From the Pythagorean Theorem, we know that |PB|²= |PA|²+ |AB|². Since both PA and AB have non-zero length, their squares are positive numbers.

If |PB|² is equal to |PA|² plus some positive number (|AB|²), it is bigger than |PA|² and thus |PB| > |PA|, for every point B other than the one where the perpendicular line meets the line l.

Proof

(1) PA ⊥l                               //Given
(2) ΔPAB is a right triangle  //Definition of a right triangle, from (1)
(3) |PB|²= |PA|²+ |AB|²              //Pythagorean Theorem
(4) |AB|²>0                             //Square of a non-zero number is positive
(5) |PB|²>|PA|²                          //(3),(4)
(6) |PB|>|PA|                            //Lines have positive lengths, so the square root is positive.