We can use the proof that in isosceles triangles the height to the base bisects the base, and get a "two-for-one," as the exact same proof shows us multiple corresponding parts that are congruent.
Problem
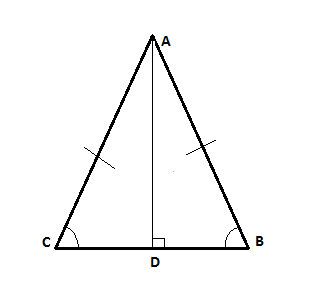
Prove that in isosceles triangle ΔABC, the height to the base, AD, bisects the apex angle.
Strategy
We will simply reuse what we have done before.
We know that AD is the height to the base, which by definition means that the angle it creates with the base (∠ADB) is a right angle, and so is ∠ADC. So ∠ADB is congruent to ∠ADC and we have found our second pair of congruent angles. We can now show that the triangles are congruent, and as a result that the angles ∠CAD and ∠BAD are congruent.
Nothing is changed in the proof steps at all!
Proof
(1) ΔABC is isosceles //Given
(2) AB=AC // Definition of an isosceles triangle
(3) ∠ACB ≅ ∠ABC // Base angles theorem
(4) m∠ADB =m∠ADC = 90° // Definition of height to base
(5) △ABD≅△ACD // angle-angle-side
(6) ∠CAD ≅ ∠BAD // Corresponding angles in congruent triangles (CPCTC)
The converse of this is also true - If the bisector of an angle in a triangle is perpendicular to the opposite side, then the triangle is isosceles.
