Two circles that have the same center point are called concentric circles. A secant is a line that interest a circle (or any other curved line) at two or more point. We will now show that a secant line that intersects both of the concentric circles creates two congruent segments between the two circles.
Problem
Two congruent circles with center at point O are intersected by a secant. Prove that AB=CD.
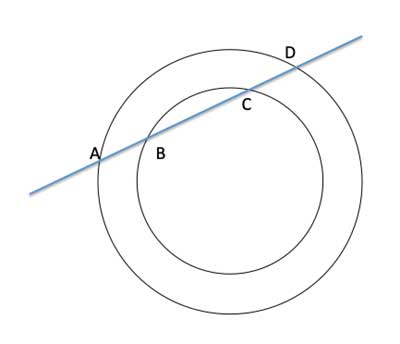
Strategy
The secant creates two chords. In the outer circle, it forms chord AD. In the inner circle, it forms chord BC (which is a sub-segment of chord AD). What do we know about chords? One property is that a diameter or radius that is perpendicular to a chord bisects that chord.
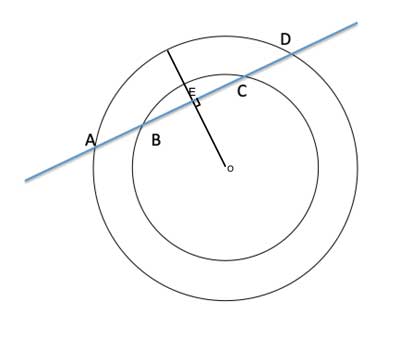
In our case, since the two circle are concentric, they have the same center point O. So if we draw such a radius from the center point O, it will bisect both AD and BC - so BE=EC and AE=ED. And with some simple math, we can show that the non-overlapping difference between the line segments is also equal.
Proof
(1) OE⊥BC //Construction
(2) BE=EC //Perpendicular radius bisects the chord
(3) AE=ED //Perpendicular radius bisects the chord
(4)AE-BE=ED-EC //(2), (3) , Subtraction property of equality
(5)AB=CD //Segment addition postulate
