In this post, we will show that chords that bisect each other are diameters of the circle.
Problem
In circle O, chord AB bisects chord CD, and chord CD bisects chord AB. Prove that AB and CD are both diameters of the circle.
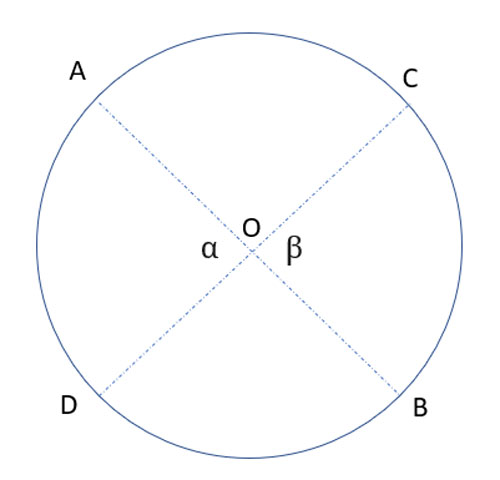
Strategy
One way to show that a chord is a diameter is to show that the two arcs formed by the chords are equal. Another way is to show that one of the arcs is subtended by a central angle measuring 180°, or equivalently, that it is subtended by an inscribed angle that measures 90° (since the inscribed angle's measure is half that of the central angle of the same arc)
In this problem, we don't know anything about the arcs, so let's see if we can prove it using inscribed angles.
We can connect the edges of the chords, forming a quadrilateral, and 4 triangles. Since the chords bisect each other, we have two pairs of equal halves of the chords, and it is easy to show that the two pairs of triangles are congruent using SAS. Then, the opposite sides of the quadrilateral are equal as corresponding sides in congruent triangles: AD=BC and DB=AC.
it follows that AD+DB = BC+AC, and the arcs of equal chord are equal, so
arc(AD)+arc(DB)= arc(BC)+arc(AC), and so arc(ADB) = arc(BCA).
Chord BA thus separates the circle into two equal arcs, so it is a diameter, and we can similarly show the arcs formed by CD are equal which means it is a diameter, too.
Proof
Here's how you prove that chords that bisect each other are diameters:
(1) AO=OB //Given
(2) CO=OD //Given
(3) ∠α≅∠β //Vertical angles
(4) △OAD ≅△OCB //(1), (2), (3), Side-Angle-Side postulate
(5) AD=CB //(4) corresponding sides of congruent triangles (CPCTC)
(6) ∠AOC ≅ ∠BOD //Vertical angles
(7) △AOC ≅△BOD //(1), (2), (6), Side-Angle-Side postulate
(8) AC=DB //(7) corresponding sides of congruent triangles (CPCTC)
(9) Arc(AC) = Arc(DB) //(8), equal chords have equal arcs
(10) Arc(AD) = Arc(CB) //(5), equal chords have equal arcs
(11) Arc(AD)+Arc(DB)= Arc(BC)+Arc(AC) //(9), (10) Additive Property of Equality
(12) Arc(ADB) = Arc(BCA) //(11)
(13) AB is a diameter //(12), diameter bisects circle into equal arcs