In a square, the diagonals bisect each other. This is a general property of any parallelogram. And as a square is a special parallelogram, which has all the parallelogram's basic properties, this is true for a square as well.
We have already proven this property for any parallelogram. And today, we will repeat this proof here specifically for square.
Problem
ABCD is a square. Show that its diagonals bisect each other, that is prove that AO=OC and BO=OD.
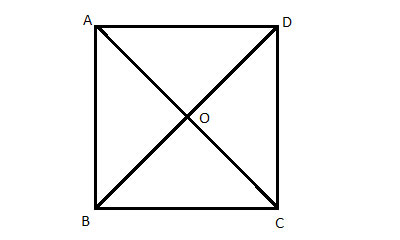
Strategy
When we attempt to prove that the diagonals of a square bisect each other, we will use congruent triangles. This is exactly what we did in the general case, and it's the simplest way to show that two line segments are equal.
In a square, all the sides are equal by definition. So if we look at the triangles formed by the diagonals and the sides of the square, we already have one equal side to use in the Angle-Side-Angles postulate.
The angles are congruent as the sides of the square are parallel, and the angles are alternate interior angles.
Proof
(1) ABCD is a square //Given
(2) AD = BC //(1) , Definition of a square, all sides are equal
(3) AD||BC //(1), a square is a parallelogram, opposite sides are parallel
(4) ∠OBC ≅ ∠ODA //Alternate Interior Angles Theorem
(5) ∠OCB ≅ ∠OAD //Alternate Interior Angles Theorem
(6) ΔOBC ≅ ΔODA // Angle-Side-Angle
(7) BO=OD // Corresponding sides in congruent triangles (CPCTC)
(8) AO=OC // Corresponding sides in congruent triangles (CPCTC)