Angle Bisector Theorem

The angle bisector is a line that divides an angle into two equal halves, each with the same angle measure.

The angle bisector theorem states that in a triangle, the angle bisector partitions the opposite side of the triangle into two segments, with a ratio that is the same as the ratio between the two sides forming the angle it bisects:

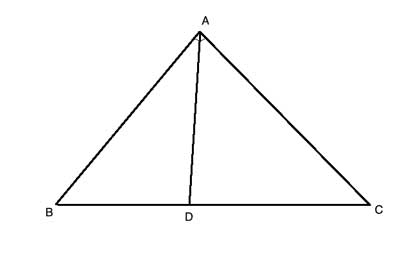
If ∠BAD≅ ∠CAD, then |BD|/|DC|=|AB|/|AC|

This is another useful tool in problems that require you to compare lengths of different line segments. [The others being similar triangles, triangles with the same height or base, or the intercept theorem].

Problem

AD is the angle bisector of angle ∠BAC in triangle △ABC (∠BAD≅ ∠CAD). Show that |BD|/|DC|=|AB|/|AC|

Strategy

Many proofs of this theorem use trigonometry and the law of sines. But here, we will provide a proof that does not rely on such advanced knowledge.

Instead, we will use one of the other tools already in our pocket for comparing ratios of line segments- triangles with the same height.

Let's look at the two triangles formed by the angle bisector, △ABD and △ADC. Both have the same height, h, from A:

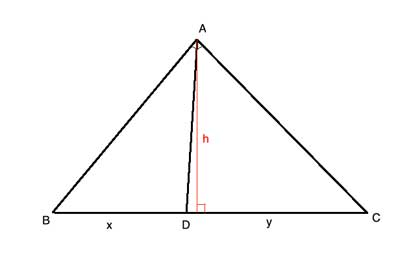
That means that the ratio of their areas will be the same as the ratio of their bases:

Area_ΔABD/ Area_ADC=|BD|/|DC|

Now, as we've seen, all points on the angle bisector are equidistant from the two sides of the angle. (This is easily proven with congruent triangles and the angle-side-angle postulate). D is such a point on the angle bisector.

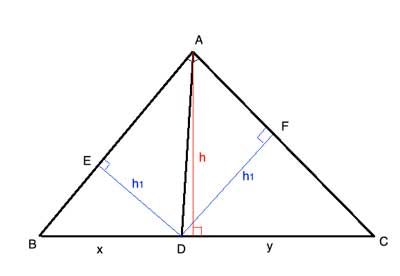
So, if we compute at the areas of these two triangles using the height from D, which is the same for both triangles, we have:

Area_ΔABD=(|AB|·h₁)/2, and Area_ΔACD=(|AC|·h₁)/2, so

Area_ΔABD/Area_ΔACD=|AB|/|AC|.

But as we saw above, Area_ΔABD/ Area_ADC=|BD|/|DC| , so |BD|/|DC|=|AB|/|AC|

Proof

(1) Area_ΔABD/ Area_ΔADC=|BD|/|DC| //ratio of areas of triangles with same height is equal to the ratio of their bases
(2) AD=AD //Common side, reflexive property of equality
(3) ∠BAD≅ ∠CAD //given, AD is the angle bisector of ∠BAC
(4) m∠DEA=m∠DFA=90° //construction
(5) ∠EDA≅ ∠FDA //(3),(4), Sum of angles in a triangle
(6)△EDA≅△FDA //(2), (3), (5), Angle-Side-Angle Postulate
(7) DE=DF=h₁ //Corresponding sides of congruent triangles (CPCTC)
(8) Area_ΔABD/Area_ΔACD=|AB|/|AC| //ratio of areas of triangles with same height is equal to the ratio of their bases
(9) |BD|/|DC|=|AB|/|AC| //(1),(8), transitive property of equality