The Triangle Midsegment Theorem states that the midsegment of a triangle is parallel to the third side, and its length is equal to half the length of the third side.
We will now prove the converse of this theorem - that if a line connecting two sides of a triangle is parallel to the third side and equal to half that side, it is a midsegment.
This is just one of several converse theorems for the triangle midsegment theorem. We also prove another converse theorem - that if a line connecting two sides of a triangle is parallel to the third side and intersects one side’s midpoint, it is a midsegment.
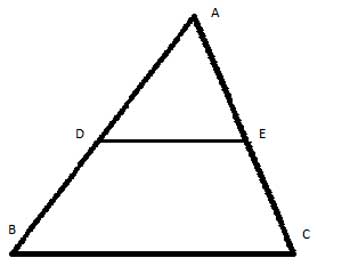
Problem
In triangle ΔABC, DE is parallel to BC, and its length is equal to half the length of BC. Show that DE is a midsegment. In other words: Show that BD=DA and CE=EA.
Strategy
Since this is a converse theorem, it is often a good strategy to solve the geometry problem by looking at how we proved the original theorem and do things in the opposite order.
We proved the original theorem here - Triangle Midsegment Theorem , and did so by constructing another triangle by extending DE to point F so that DE=EF. Let's do that here, as well:

Now, since DE=EF, and DE is half of BC, DF should be equal to BC. We now have a quadrilateral, DFCB, in which there is a pair of opposite sides (DF and BC) which are both parallel (given) and equal in length (we constructed DF that way), and as we have shown such a quadrilateral is a parallelogram.
If DFCB is a parallelogram, BD=CF, and BD||CF, as opposite sides of a parallelogram.
Continuing to work backward from the way we proved the original theorem, we will now show the triangles ΔADE and ΔCFE are congruent, and from this show that CE=EA, and also that CF=AD, and as a result BD=AD.
Proof
(1) DE=EF //Construction
(2) DE= ½BC //Given
(3) EF = ½BC //(1), transitive property of equality
(4) DE+EF= ½BC+ ½BC //Add (2) and (3)
(5) DF = BC //Simplify (4)
(6) DE||BC //Given
(7) DFCB is a parallelogram //(5), (6), quadrilateral with two sides parallel and equal
(8) BD=CF //(7), Opposite sides of parallelogram
(9) BD||CF //(7), Opposite sides of parallelogram
(10) ∠DAE ≅ ∠FCE // Alternate Interior Angles Theorem
(11) ∠AED ≅ ∠CEF // Vertical angles
(12) DE=EF //Construction
(13) ΔADE ≅ ΔCFE // Angle-Angle-Side
(14) CE=EA // corresponding sides in congruent triangles, (CPCTC)
(15) CF=DA // corresponding sides in congruent triangles, (CPCTC)
(16) CF=BD // (8)
(17) DA=BD // (15), (16), transitive property of equality
