Area of Parallelogram Given Diagonals and a Side

The basic formula for calculating the area of a parallelogram is the length of one side times the height of the parallelogram to that side.

But what do we do when we do not have these measurements (side, height)? What if instead we are presented with the length of one side, and the length of both diagonals?

Let's see how we can still compute the area of the parallelogram in that case, in the following problem.

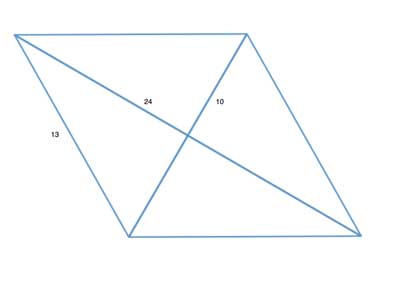
Problem

A parallelogram has a side of length 13 units, and its diagonal lengths are 24 units and 10 units. Find its area.

Strategy

There are two ways to start thinking about this problem, and both will lead us to the same point and the solution.

Since we have both the diagonals, we can start by thinking about the properties of diagonals in parallelograms - they bisect each other. So if we have diagonals of 24 and 10 units, they bisect each other into segments of 12 units and 5 units, respectively:

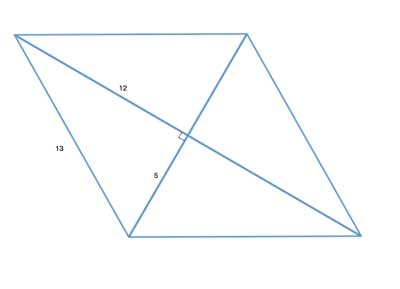
So now we have a triangle with sides 5, 12 and 13 - a Pythagorean Triple, which means the triangle is a right triangle, and we can easily compute its area as leg x leg /2, or 5x12/2=30.

But if m∠AOB=90°, then m∠AOD=90°, as ∠AOB and ∠AOD are a linear pair which add up to 180°. Triangles ΔAOB and ΔAOD are then congruent (by Side-Angle-Side), as are triangles ΔAOB and ΔCOB (also Side-Angle-Side). So we have 4 triangles of area 30 making up the area of the parallelogram, whose area is thus 4x30=120.

Another way to think about the problem is to remember that if the parallelogram is a rhombus, then its area is the product of the diagonals divided by two. That is because a rhombus is also a kite, and we've shown that the area of a kite is half the product of its diagonals.

So if we prove the parallelogram is a rhombus, we can use that directly. We can proceed to prove that this parallelogram is indeed a rhombus, using the fact that if a parallelogram's diagonals are perpendicular, it is a rhombus - and we've shown above that these diagonals are indeed perpendicular.

So the areas of the parallelogram is (diagonal x diagonal /2 ), or 24x10/2=120, as above.

Solution

(1) AC=24 //Given
(2) BD=10 //Given
(3) AO=OC=12 //Diagonals of a parallelogram bisect each other
(4) BO=OD=5 //Diagonals of a parallelogram bisect each other
(5) AB=13 //Given
(6) m∠AOB=90° //(3), (4), (5), Converse of the Pythagorean theorem (5,12,13 are a Pythagorean Triple)
(7) AC⊥DB  //(6), definition of perpendicular lines
(8) ABCD is a rhombus //a parallelogram with perpendicular diagonals is a rhombus
(9) Area_ABCD=|AC|·|DB|/2 //Area of a rhombus is the product of the diagonals, divided by two
(10) Area_ABCD =24·10/2=120 square units //(1),(2), (9)

So in this case, we have diagonals and a side of a parallelogram which happen to form a Pythagorean triple. This makes for an easy calculation of the area of the parallelogram. But what about other parallelograms, where the diagonals are not perpendicular?

It turns out we can find out the area of the parallelogram for those cases, too. We'll just have to use a little more calculations known as Heron's formula for the area of a triangle which is not a right triangle.